Question

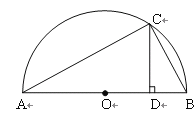
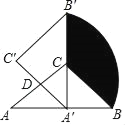
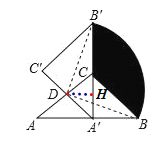
【题目】如图，在△ABC中，∠ACB＝90°，AC＝BC＝2，将△ABC绕AC的中点D逆时针旋转90°得到△A′B′C′，其中点B的运动路径为，则图中阴影部分的面积为（　　）

A.π﹣B.2C.D.

Answer 1

【答案】A

【解析】

先利用勾股定理求出DB′，A′B′再根据S阴影=S扇形BDB′-S△DBC-S△DB′C，计算即可.

解：连接DB，DB′，作DH⊥A′B′，△ABC绕AC的中点D逆时针旋转90°得到△A'B′C'，此时点A′在斜边AB上，CA′⊥AB，

∵∠C′A′B′=45°，

∴DH=sin45°×A′D=×1=，

∵BC=2，CD=1，

∴DB＝＝，

∵AC＝BC＝2，

∴AB=A′B′＝＝2，

∴B′C=2﹣=，

∴S阴＝﹣1×2÷2﹣×÷2＝π﹣．

故选：A．