题目内容
【题目】如果三角形有一边上的中线长恰好等于这边的长,那么称这个三角形为“好玩三角形”.
(1)请用直尺和圆规画一个“好玩三角形”;
(2)如图1,在Rt△ABC中,∠C=90°,tanA= ![]() ,求证:△ABC是“好玩三角形”;
,求证:△ABC是“好玩三角形”;
(3)如图2,已知菱形ABCD的边长为a,∠ABC=2β,点P,Q从点A同时出发,以相同速度分别沿折线AB﹣BC和AD﹣DC向终点C运动,记点P经过的路程为s.
①当β=45°时,若△APQ是“好玩三角形”,试求![]() 的值;
的值;
②当tanβ的取值在什么范围内,点P,Q在运动过程中,有且只有一个△APQ能成为“好玩三角形”.请直接写出tanβ的取值范围.
(4)依据(3)的条件,提出一个关于“在点P,Q的运动过程中,tanβ的取值范围与△APQ是‘好玩三角形’的个数关系”的真命题(“好玩三角形”的个数限定不能为1)

【答案】(1)见解析 (2)见解析 (3)①![]() ②
②![]() <tanβ<2
<tanβ<2
(4)在P、Q的运动过程中,当0<tanβ<![]() 时,使得△APQ成为“好玩三角形”的个数为2.
时,使得△APQ成为“好玩三角形”的个数为2.
【解析】解:(1)如图1,

①作一条线段AB,
②作线段AB的中点O,
③以点O为圆心,AB长为半径画圆,
④在圆O上取一点C(点E、F除外),连接AC、BC.
∴△ABC是所求作的三角形.
(2)如图2,
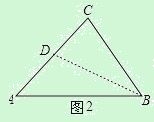
取AC的中点D,连接BD.
∵∠C=90°,tanA= ![]() ,
,
∴![]()
∴设BC= ![]() x,则AC=2x,
x,则AC=2x,
∵D是AC的中点,
∴CD= ![]() AC=x
AC=x
∴BD= ![]() =
= ![]() =2x,
=2x,
∴AC=BD
∴△ABC是“好玩三角形”;
(3)①当β=45°,点P在AB上时,
∴∠ABC=2β=90°,
∴△APQ是等腰直角三角形,不可能是“好玩三角形”,
如图3,当P在BC上时,连接AC交PQ于点E,延长AB交QP的延长线于点F,
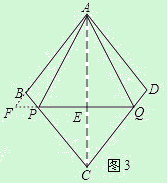
∵四边形ABCD是菱形,∠ABC=2β=90°,
∴四边形ABCD是正方形,
∴AB=BC,∠ACB=∠ACD=45°,
∴∠CAB=∠ACP,
∵PC=CQ,∠ACB=∠ACD,
∴∠AEF=∠CEP=90°,
∴△AEF∽△CEP,且△AEF、△CEP和△BFP都是等腰直角三角形,
∴![]() .
.
∵PE=CE,
∴![]() .
.
(Ⅰ)当底边PQ与它的中线AE相等时,即AE=PQ时,
![]() ,
,
∴![]() ,
,
(Ⅱ)当腰AP与它的中线QM相等,即AP=QM时,
作QN⊥AP于N,如图4
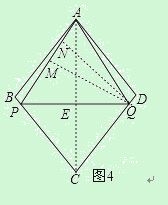
∵AP=QM=AQ
∴MN=AN= ![]() MP.
MP.
∴QN= ![]() MN,
MN,
∴tan∠APQ= ![]() ,
,
∴tan∠APE= ![]() ,
,
∴![]() =
= ![]()
②由①可知,当AE=PQ和AP=QM时,有且只有一个△APQ能成为“好玩三角形”,
∴![]() <tanβ<2时,有且只有一个△APQ能成为“好玩三角形”.
<tanβ<2时,有且只有一个△APQ能成为“好玩三角形”.
(4)由(3)可以知道:在P、Q的运动过程中,当0<tanβ<![]() 时,使得△APQ成为“好玩三角形”的个数为2.
时,使得△APQ成为“好玩三角形”的个数为2.
(1)先画一条线段AB,再确定AB的中点O,以点O为圆心,AB为半径画圆,在圆O上取一点C,连接AC、BC,则△ABC是所求作的三角形;
(2)取AC的中点D,连接BD,设BC= ![]() x,根据条件可以求出AC=2x,由三角函数可以求出BD=2x,从而得出AC=BD,从而得出结论;
x,根据条件可以求出AC=2x,由三角函数可以求出BD=2x,从而得出AC=BD,从而得出结论;
(3)①当β=45°时,分情况讨论,P点在AB上时,△APQ是等腰直角三角形,不可能是“好玩三角形”,当P在BC上时,延长AB交QP的延长线于点F,可以求出![]() ,再分情况讨论,当AE=PQ和AP=QM时,求出
,再分情况讨论,当AE=PQ和AP=QM时,求出![]() 的值;
的值;
②根据①求出的两个![]() 的值可以求出tanβ的取值范围;
的值可以求出tanβ的取值范围;
(4)由(3)可以得出“在P、Q的运动过程中,当0<tanβ<![]() 时,使得△APQ成为‘好玩三角形’的个数为2”是真命题.
时,使得△APQ成为‘好玩三角形’的个数为2”是真命题.

 高中必刷题系列答案
高中必刷题系列答案
