题目内容
【题目】阅读下面的材料:
在平面几何中,我们学过两条直线平行的定义.下面就两个一次函数的图象所确定的两条直线,给出它们平行的定义:设一次函数y=k1x+b1(k1≠0)的图象为直线l1,一次函数y=k2x+b2(k2≠0)的图象为直线l2,若k1=k2,且b1≠b2,我们就称直线l1与直线l2互相平行.

解答下面的问题:
(1)求过点P(1,4)且与已知直线y=-2x-1平行的直线的函数表达式,并画出直线l的图象;
(2)设直线l分别与y轴、x轴交于点A、B,如果直线![]() :y=kx+t ( t>0)与直线l平行且交x轴于点C,求出△ABC的面积S关于t的函数表达式.
:y=kx+t ( t>0)与直线l平行且交x轴于点C,求出△ABC的面积S关于t的函数表达式.
【答案】(1)y=—2x+6,直线的图象如图:
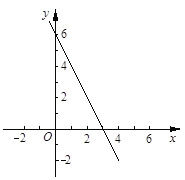
(2)△![]() 的面积
的面积![]() 关于的函数表达式为
关于的函数表达式为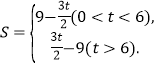
【解析】
试题(1)设直线l的函数表达式为y=k x+b,根据平行的性质可得k=—2,再根据直线l过点(1,4),即可求得直线l的函数表达式,最后根据描点法即可做出直线的图象;
(2)先分别求得直线l分别与y轴、x轴的交点A、B的坐标,再根据l∥![]() ,可设直线
,可设直线![]() 为y=—2x+t,从而表示出C点的坐标为(
为y=—2x+t,从而表示出C点的坐标为(![]() ,0),由t>0可判断C点在x轴的正半轴上,再分C点在B点的左侧与C点在B点的右侧两种情况结合三角形的面积公式分析即可.
,0),由t>0可判断C点在x轴的正半轴上,再分C点在B点的左侧与C点在B点的右侧两种情况结合三角形的面积公式分析即可.
(1)设直线l的函数表达式为y=k x+b.
∵直线l与直线y=—2x—1平行,∴k=—2.
∵直线l过点(1,4),∴—2+b=4,∴b=6.
∴直线l的函数表达式为y=—2x+6,直线的图象如图:
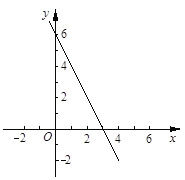
(2)∵直线l分别与y轴、x轴交于点A、B,
∴点A、B的坐标分别为(0,6)、(3,0).
∵l∥![]() ,∴直线
,∴直线![]() 为y=—2x+t.
为y=—2x+t.
∴C点的坐标为(![]() ,0).
,0).
∵t>0,
∴![]() >0.
>0.
∴C点在x轴的正半轴上.
当C点在B点的左侧时,![]() ;
;
当C点在B点的右侧时,![]() .
.
∴△![]() 的面积
的面积![]() 关于的函数表达式为
关于的函数表达式为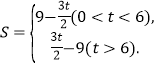

 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案