题目内容
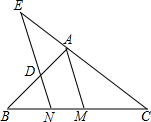
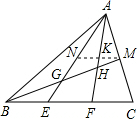
如图△ABC中，E、F为BC的三等份点，M为AC的中点，BM与AE、AF分别交于G、H，则BG：GH：HM=______．
过点M作MK∥BC，交AF，AE分别于K，N，
∵M是AC的中点，
∴
=
=
=
=
，
∵E、F是BC的三等分点，
∴BE=EF=FC，
∴MN=2NK，
∵
=
=
，
=
=1，
∴MH=
BH，MG=BG，
设MH=a，BH=4a，BG=GM=
，
∴GH=GM-MN=
，
∴BG：GH：HM=
：
：a=5：3：2．
故答案为：5：3：2．
∵M是AC的中点，
∴
| MN |
| EC |
| NK |
| EF |
| AN |
| AE |
| AM |
| AC |
| 1 |
| 2 |
∵E、F是BC的三等分点，
∴BE=EF=FC，
∴MN=2NK，
∵
| MH |
| BH |
| MK |
| BF |
| 1 |
| 4 |
| MG |
| BG |
| MN |
| BE |
∴MH=
| 1 |
| 4 |
设MH=a，BH=4a，BG=GM=
| 5a |
| 2 |
∴GH=GM-MN=
| 3a |
| 2 |
∴BG：GH：HM=
| 5a |
| 2 |
| 3a |
| 2 |
故答案为：5：3：2．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
