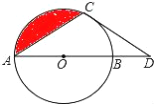
题目内容
【题目】已知:如图,AB∥CD,∠A=∠D,试说明 AC∥DE 成立的理由.
(下面是彬彬同学进行的推理,请你将彬彬同学的推理过程补充完整.)
解:∵AB∥CD (已知)
∴∠A=(两直线平行,内错角相等)
又∵∠A=∠D()
∴ =(等量代换)
∴AC∥DE ()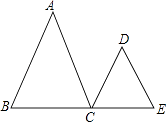
【答案】∠ACD;已知;∠ACD;∠D;内错角相等,两直线平行
【解析】解:∵AB∥CD (已知),
∴∠A=∠ACD(两直线平行,内错角相等),
又∵∠A=∠D( 已知),
∴∠ACD=∠D(等量代换),
∴AC∥DE ( 内错角相等,两直线平行).
所以答案是∠ACD;已知;ACD;D;内错角相等,两直线平行.
【考点精析】通过灵活运用平行线的判定与性质,掌握由角的相等或互补(数量关系)的条件,得到两条直线平行(位置关系)这是平行线的判定;由平行线(位置关系)得到有关角相等或互补(数量关系)的结论是平行线的性质即可以解答此题.

练习册系列答案
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
【题目】某政府部门进行公务员招聘考试,其中三人中录取一人,他们的成绩如下:
人 | 测试成绩 | ||
题目 | 甲 | 乙 | 丙 |
文化课知识 | 74 | 87 | 69 |
面试 | 58 | 74 | 70 |
平时表现 | 87 | 43 | 65 |
(1)按照平均成绩甲、乙、丙谁应被录取?
(2)若按照文化课知识、面试、平时表现的成绩已4:3:1的比例录取,甲、乙、丙谁应被录取?