题目内容
如图,已知抛物线y=ax2+bx-4与x轴交于A、B两点,与y轴交于C点,经过A、B、C三点的圆的圆心M(1,m)恰好在此抛物线的对称轴上,⊙M的半径为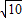 .
.(1)求m的值及抛物线的解析式;
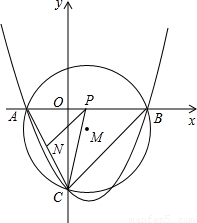
(2)点P是线段AB上的一个动点,过点P作PN∥BC,交AC于点N,连接CP,当△PNC的面积最大时,求点P的坐标;
(3)点D(2,k)在(1)中抛物线上,点E为抛物线上一动点,在x轴上是否存在点F,使以A、D、E、F为顶点的四边形是平行四边形,如果存在,直接写出所有满足条件的点F的坐标,若不存在,请说明理由.
【答案】分析:(1)过M作MK⊥y轴,连接MC,由勾股定理求出CK的值,进而求出OK的值,即M点的纵坐标的长度,问题得解;
(2)设点P的坐标为(m,0),过点N作NH⊥x轴于点H,因为BC∥PN,所以△APN∽△ABC,利用相似三角形的性质:对应边的比值相等,进而用含有m的代数式表示出NH,再利用S△PNC=S△ACP-S△APN求出三角形PNC的面积,最后利用二次函数的性质可求出当△PNC的面积最大时,点P的坐标;
(3)存在.首先根据已知条件求出D的坐标,然后讨论:当AF为平行四边形的边时,接着根据平行四边形的性质得到F的坐标;当AF为平行四边形的对角线时,分别求出满足条件的F点的坐标即可.
解答:解:(1)过M作MK⊥y轴,连接MC,
由勾股定理得CK=3,
∴OK=1,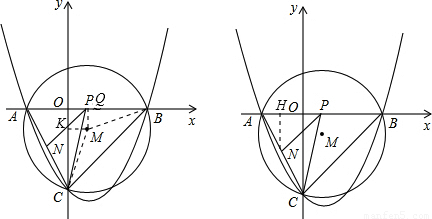
∴m=-1.
过点M作MQ⊥x轴,连接MB,
由勾股定理得BQ=3,
∴B(4,0),
又M在抛物线的对称轴上,
∴A(-2,0),
∴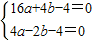 ,
,
解得: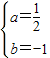 ,
,
∴抛物线的解析式为: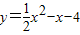 ;
;
(2)设点P的坐标为(m,0),过点N作NH⊥x轴于点H(如图).
∵点A的坐标为(-2,0),点B的坐标为(4,0),
∴AB=6,AP=m+2,
∵BC∥PN,
∴△APN∽△ABC,
∴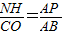 ,
,
∴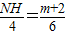 ,
,
∴NH= (m+2),
(m+2),
∴S△PNC=S△ACP-S△APN= AP•OC-
AP•OC- AP•HN=
AP•HN= (m+2)[4-
(m+2)[4- (m+2)]=-
(m+2)]=- m2+
m2+ m+
m+ =-
=- (m-1)2+3,
(m-1)2+3,
∴当m=1时,S△PNC有最大值3.此时,点P的坐标为(1,0);
(3)在x轴上存在点F,使以A、D、E、F为顶点的四边形是平行四边形.
F1(0,0)、F2(-4,0)、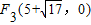 、
、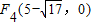 .
.
点评:此题是二次函数的综合题,分别考查了待定系数法确定函数的解析式、平行四边形的性质及轴对称的性质,综合性比较强,要求学生有很强的综合分析问题,解决问题的能力,同时相关的基础知识也熟练掌握.
(2)设点P的坐标为(m,0),过点N作NH⊥x轴于点H,因为BC∥PN,所以△APN∽△ABC,利用相似三角形的性质:对应边的比值相等,进而用含有m的代数式表示出NH,再利用S△PNC=S△ACP-S△APN求出三角形PNC的面积,最后利用二次函数的性质可求出当△PNC的面积最大时,点P的坐标;
(3)存在.首先根据已知条件求出D的坐标,然后讨论:当AF为平行四边形的边时,接着根据平行四边形的性质得到F的坐标;当AF为平行四边形的对角线时,分别求出满足条件的F点的坐标即可.
解答:解:(1)过M作MK⊥y轴,连接MC,
由勾股定理得CK=3,
∴OK=1,

∴m=-1.
过点M作MQ⊥x轴,连接MB,
由勾股定理得BQ=3,
∴B(4,0),
又M在抛物线的对称轴上,
∴A(-2,0),
∴
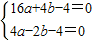 ,
,解得:
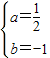 ,
,∴抛物线的解析式为:
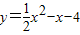 ;
;(2)设点P的坐标为(m,0),过点N作NH⊥x轴于点H(如图).
∵点A的坐标为(-2,0),点B的坐标为(4,0),
∴AB=6,AP=m+2,
∵BC∥PN,
∴△APN∽△ABC,
∴
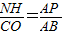 ,
,∴
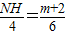 ,
,∴NH=
 (m+2),
(m+2),∴S△PNC=S△ACP-S△APN=
 AP•OC-
AP•OC- AP•HN=
AP•HN= (m+2)[4-
(m+2)[4- (m+2)]=-
(m+2)]=- m2+
m2+ m+
m+ =-
=- (m-1)2+3,
(m-1)2+3,∴当m=1时,S△PNC有最大值3.此时,点P的坐标为(1,0);
(3)在x轴上存在点F,使以A、D、E、F为顶点的四边形是平行四边形.
F1(0,0)、F2(-4,0)、
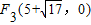 、
、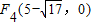 .
.点评:此题是二次函数的综合题,分别考查了待定系数法确定函数的解析式、平行四边形的性质及轴对称的性质,综合性比较强,要求学生有很强的综合分析问题,解决问题的能力,同时相关的基础知识也熟练掌握.

练习册系列答案
相关题目
 C(0,3).
C(0,3). 、C(0,-3)两点,与x轴交于另一点B.
、C(0,-3)两点,与x轴交于另一点B. (2013•衡阳)如图,已知抛物线经过A(1,0),B(0,3)两点,对称轴是x=-1.
(2013•衡阳)如图,已知抛物线经过A(1,0),B(0,3)两点,对称轴是x=-1. 如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,且抛物线经过A(-1,0)、C(0,-3)两点,与x轴交于另一点B.
如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,且抛物线经过A(-1,0)、C(0,-3)两点,与x轴交于另一点B. 如图,已知抛物线y=ax2+bx+c的顶点是(-1,-4),且与x轴交于A、B(1,0)两点,交y轴于点C;
如图,已知抛物线y=ax2+bx+c的顶点是(-1,-4),且与x轴交于A、B(1,0)两点,交y轴于点C;