题目内容
【题目】已知抛物线![]() 与x轴交于A、B两点(A在B的左侧),与y轴的正半轴交于点C,顶点为D,对称轴与直线BC交于点E,且CE :BE=1 :2,连接BD,作CF//AB交抛物线对称轴于点H,交BD于点F.
与x轴交于A、B两点(A在B的左侧),与y轴的正半轴交于点C,顶点为D,对称轴与直线BC交于点E,且CE :BE=1 :2,连接BD,作CF//AB交抛物线对称轴于点H,交BD于点F.
(1)写出A、B两点的坐标:A( , ),B( , )
(2)若四边形BEHF的面积为![]() ,求抛物线的函数表达式;
,求抛物线的函数表达式;
(3)在(2)的条件下,抛物线对称轴上是否存在点M,使得∠CMF=∠CBF,若存在,请求出M点的坐标;若不存在,请说明理由.
【答案】(1)-1,0;3,0;(2)y=﹣x2 + 2x + 3 ;(3)![]()
【解析】
(1)设对称轴与x轴交于点G,根据CE:BE=1:2得出OG:BG=1:2,再结合对称轴为直线x=1可得OG和BG的长,从而得到点B坐标,再利用两根之和得出点A坐标;
(2)设抛物线表达式为![]() ,得到点C和点D的坐标,求出BD和BC的表达式得到E和F的坐标,再利用S四边形BEFH=S△BCF-S△CHE得到方程求出a的值即可;
,得到点C和点D的坐标,求出BD和BC的表达式得到E和F的坐标,再利用S四边形BEFH=S△BCF-S△CHE得到方程求出a的值即可;
(3)根据(2)得出B,C,F的坐标,设△BCF的外接圆圆心为点P,根据题意设点P坐标为(m,m),由PC2=PF2,列出方程求出m值,再根据M在抛物线对称轴上,∠CMF=∠CBF,设M(1,n),根据PM2=PC2,列出方程求出n值即可得到结果.
解:(1)如图,设对称轴与x轴交于点G,
∵CE:BE=1:2,DG∥y轴,
可得OG:BG=1:2,
在抛物线![]() 中,
中,
对称轴为直线x=1,
∴OG=1,BG=2,
∴B(3,0),
则点A的横坐标为:2-3=-1,
则A(-1,0),
故答案为:A(-1,0), B(3,0);
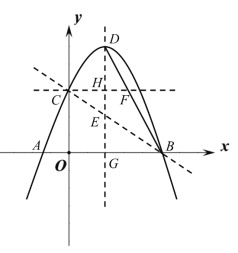
(2)设![]() ,
,
得:C(0,﹣3a),D(1,﹣4a),
∵B(3,0),设BD的表达式为:y=kx+b,将B和C代入,
![]() ,解得:
,解得:![]() ,
,
∴BD的表达式为:![]() ,
,
∵CF//AB,
令y=-3a,解得x=![]() ,
,
∴![]() ,
,
同理可得:BC的表达式为:![]() ,
,
令x=1,则y=-2a,
∴E(1,-2a),
S四边形BEFH=S△BCF-S△CHE=![]() =
=![]() ,
,
解得:a=﹣1,
∴y=﹣x2 + 2x + 3;
(3)由(2)可得:C(0,3),B(3,0),F(![]() ,3),
,3),
∵OB=OC,
设△BCF的外接圆圆心为点P,可知点P到点B的距离等于点P到点C的距离,
可知点P在直线y=x上,
∴设点P坐标为(m,m),
∵PC2=PF2,
∴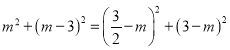 ,
,
解得:m=![]() ,
,
∴P(![]() ,
,![]() ),
),
∵M在抛物线对称轴上,∠CMF=∠CBF,
∴M在△BCF的外接圆上,
设M(1,n),
则有PM2=PC2,
∴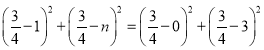 ,
,
解得n=![]() (舍)或
(舍)或![]() ,
,
∴![]() .
.

 巧学巧练系列答案
巧学巧练系列答案 课课练江苏系列答案
课课练江苏系列答案【题目】现在,步行运动深受广大健身爱好者的喜爱. 通过“微信运动”可以查询微信好友当天的行走步数.实验中学张老师根据该校![]() 名教师某日“微信运动”中的行走步数,绘制成如下两张统计表(不完整).
名教师某日“微信运动”中的行走步数,绘制成如下两张统计表(不完整).
步数 | 频数 | 频率 |
|
| 0.2 |
| 19 | 0.38 |
|
| 0.3 |
| 4 |
|
| 2 | 0.04 |
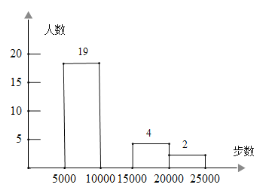
(1)写出左表中![]() 、
、![]() 、
、![]() 的值,并补全条形统计图;
的值,并补全条形统计图;
(2)实验中学所在的某县有![]() 名教师,用张老师调查的样本数据估计该县当天行走步数不少于
名教师,用张老师调查的样本数据估计该县当天行走步数不少于![]() 步的教师有多少人?
步的教师有多少人?
(3)在该校![]() 名教师中,随机选取当天行走步数不少于
名教师中,随机选取当天行走步数不少于![]() 步的
步的![]() 名教师参加“我运动,我健康”的征文活动,求选中的
名教师参加“我运动,我健康”的征文活动,求选中的![]() 名教师的行走步数都不小于
名教师的行走步数都不小于![]() 步的概率.
步的概率.
【题目】华联超市用6000元购进甲、乙两种商品,其中乙商品的件数比甲商品件数的![]() 多15件,甲、乙两种商品的进价和售价如下表:(注:获利=售价﹣进价)
多15件,甲、乙两种商品的进价和售价如下表:(注:获利=售价﹣进价)
甲 | 乙 | |
进价(元/件) | 22 | 30 |
售价(元/件) | 29 | 40 |
(1)该商场购进甲、乙两种商品各多少件?
(2)该超市将购进的甲、乙两种商品全部卖完后一共可获得多少利润?