题目内容
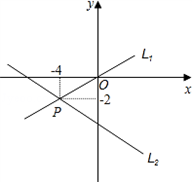
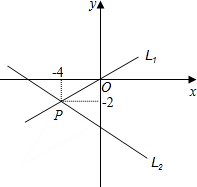 如图,直线L1上所有的点坐标都是方程
如图,直线L1上所有的点坐标都是方程| 1 |
| 2 |
| 1 |
| 4 |
|
|
|
分析:因为直线l1上所有点的坐标都是方程
x-y=0的解,直线l2上所有点的坐标都是
x+y=-3的解,所以,直线l1与l2的直线方程分别为
x-y=0、
x+y=-3,故l1与l2的交点的坐标为方程组
的解.
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
|
解答:解:由直线l1和l2的交点位置可知,直线l1和l2的交点坐标为(-4,-2),
所以
的解是
.
故答案为
.
所以
|
|
故答案为
|
点评:本题要求利用图象求解各问题,根据图象观察,得出结论.要认真体会直线方程的交点与方程组的解之间的关系.

练习册系列答案
相关题目
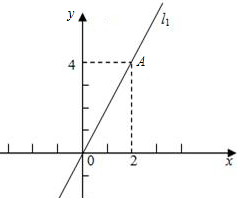 如图,在平面直角坐标系xoy中,直线l1经过点O和点A,将直线l1绕点O逆时针旋转90°,再向上平移2个单位长度得到直线l2.
如图,在平面直角坐标系xoy中,直线l1经过点O和点A,将直线l1绕点O逆时针旋转90°,再向上平移2个单位长度得到直线l2.
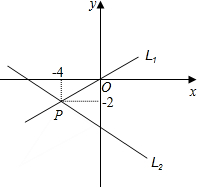 如图,直线L1上所有的点坐标都是方程
如图,直线L1上所有的点坐标都是方程 x-y=0的解,直线L2上所有点的坐标都是方程
x-y=0的解,直线L2上所有点的坐标都是方程 x+y=-3的解,直线L1和直线L2相交于点P,那么
x+y=-3的解,直线L1和直线L2相交于点P,那么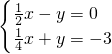 的解是________.
的解是________. x﹣y=0的解,直线L2上所有点的坐标都是方程
x﹣y=0的解,直线L2上所有点的坐标都是方程 x+y=﹣3的解,直线L1和直线L2相交于点P,那么
x+y=﹣3的解,直线L1和直线L2相交于点P,那么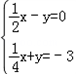 的解是( )
的解是( )