题目内容

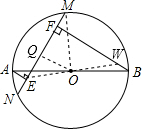
如图，AB是⊙O的直径，MN是弦，AE⊥MN于E，BF⊥MN于F，AB=10，MN=8，求BF-AE的值．

连接EO，并延长交BF于W，过O作OQ⊥MN于Q，
∵AE⊥MN，BF⊥MN，
∴AE∥OQ∥BF，
∵AO=OB，
∴EO=OW，EQ=QF，
∵AE∥BF，
∴△AEO∽△BWO，
∴
AE
BW
=
AO
OB
，
∵AO=BO，
∴AE=BW，
∴BF-AE=BF-BW=FW，
∵OQ⊥MN，OQ过O，
∴MQ=NQ=
1
2
MN=4，
∵直径AB=10，
∴OM=5，
在Rt△MQO中，由勾股定理得：OQ=3，
∵EQ=QF，EO=OW，
∴WF=2OQ=6，
即BF-AE=6．
练习册系列答案
相关题目
某居民小区一处圆柱形的输水管道破裂，维修人员为更换管道，需确定管道圆形截面的半径，如图是水平放置的破裂管道有水部分的截面．
（1）请你用直尺和圆规补全这个输水管道的圆形截面（保留作图痕迹）；
（2）若这个输水管道有水部分的水面宽AB=8cm，水面最深地方的高度为2cm，求这个圆形截面的半径．
已知：⊙O的直径为10cm，圆心O到弦AB的距离为3cm，则AB的长为（　　）
A．
91
cm		B．4cmC．2
91
cm		D．8cm
在直角坐标系中，⊙M经过点A（-4，0），B（0，2），O（0，O），则M点的坐标是（　　）
A．（-2，O）B．（0，1）C．（-2，1）D．（2，1）
过圆上一点引两条互相垂直的弦，如果圆心到两条弦的距离分别是2和3，那么这个圆的直径是______．
圆的半径为13cm，两弦AB∥CD，AB=24cm，CD=10cm，则两弦AB，CD的距离是______．
如图，AB是⊙O的直径，BC是⊙O的弦，半径OD⊥BC，垂足为E，若BC=6
3
，DE=3．
（1）图中有很多结论，例如：OA=OC=OD=OB等，请任意写出另外两个正确的结论；
（2）求⊙O的半径．
图中的三块阴影部分由两个半径为1的圆及其外公切线分割而成，如果中间一块阴影的面积等于上下两块面积之和，则这两圆的公共弦长是（　　）
A．
5
2
B．
6
2
C．
1
2
25-π2
D．
1
2
16-π2
如图，已知⊙O的直径AB⊥弦CD于点E，下列结论中一定正确的是（　　）
A．AE=OEB．CE=DEC．OE=CED．∠AOC=60°

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网