题目内容
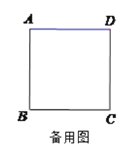
【题目】如图,四边形ABCD是边长为3的正方形,点E在边AD所在的直线上,连接CE,以CE为边,作正方形CEFG(点C、E、F、G按逆时针排列),连接BF.
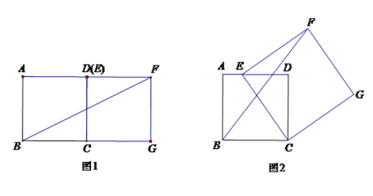
(1)如图1,当点E与点D重合时,BF的长为 ;
(2)如图2,当点E在线段AD上时,若AE=1,求BF的长;(提示:过点F作BC的垂线,交BC的延长线于点M,交AD的延长线于点N.)
(3)当点E在直线AD上时,若AE=4,请直接写出BF的长.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】
(1)利用勾股定理即可求出.
(2)过点F作FH⊥AD交AD于的延长线于点H,作FM⊥AB于点M,证出![]() ,进而求得MF,BM的长,再利用勾股定理,即可求得.
,进而求得MF,BM的长,再利用勾股定理,即可求得.
(3)分两种情况讨论,同(2)证得三角形全等,再利用勾股定理即可求得.
(1)由勾股定理得:![]()
(2)过点F作FH⊥AD交AD于的延长线于点H,作FM⊥AB于点M,如图2所示:
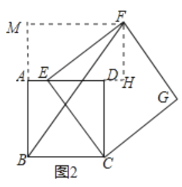
则FM=AH,AM=FH
∵四边形CEFG是正方形 ∴EC=EF,∠FEC=90° ∴∠DEC+∠FEH=90°,
又∵四边形![]() 是正方形 ∴∠ADC=90° ∴∠DEC+∠ECD=90°,∴∠ECD=∠FEH
是正方形 ∴∠ADC=90° ∴∠DEC+∠ECD=90°,∴∠ECD=∠FEH
又∵∠EDC=∠FHE=90°,∴![]() ∴FH=ED EH=CD=3
∴FH=ED EH=CD=3
∵AD=3,AE=1,ED=AD-AE=3-1=2,∴FH=ED=2
∴MF=AH=1+3=4,MB=FH+CD=2+3=5
在Rt△BFM中,BF=![]()
(3)分两种情况:
①当点E在边AD的左侧时,过点F作FM⊥BC交BC的反向延长线于点M,交DE于点N.如图3所示:
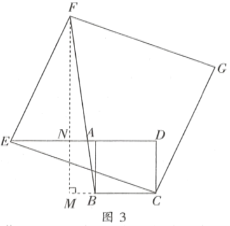
同(2)得:![]()
∴EN=CD=3,FN=ED=7
∵AE=4∴AN=AE-EN=4-3=1
∴MB=AN=1 FM=FN+NM=7+3=10
在![]() 中
中
由勾股定理得:![]()
②当点E在边AD的右侧时,过点F作FN⊥AD交AD的延长线于点N,交BC延长线于M,如图4所示:

同理得: ![]()
∴NF=DE=1,EN=CD=3
∴FM=3-1=2,CM=DN=DE+EN=1+3=4
∴BM=CB+CM=3+4=7
在![]() 中
中
由勾股定理得:![]()
故BF的长为![]()

 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案