题目内容
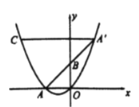
【题目】如图是一副眼镜镜片下半部分轮廓对应的两条抛物线关于y轴对称.AB∥x轴,AB=4cm,最低点C在x轴上,高CH=1cm,BD=2cm.则右轮廓线DFE所在抛物线的函数解析式为__________________________________.

【答案】y= ![]() (x﹣3)2
(x﹣3)2
【解析】
由B、D关于y轴对称,CH=1cm,BD=2cm可得到D点坐标为(1,1),由AB=4cm,最低点C在x轴上,则AB关于直线CH对称,可得到左边抛物线的顶点C的坐标为(-3,0),于是得到右边抛物线的顶点F的坐标为(3,0),然后设顶点式利用待定系数法求抛物线的解析式.
解:∵高CH=1cm,BD=2cm,AB∥x轴,
而B、D关于y轴对称,
∴D点坐标为(1,1),
∵AB∥x轴,AB=4cm,最低点C在x轴上,
∴AB关于直线CH对称,
∴左边抛物线的顶点C的坐标为(-3,0),
∴右边抛物线的顶点F的坐标为(3,0),
设右边抛物线的解析式为y=a(x-3)2,
把D(1,1)代入得1=a×(1-3)2,解得a=![]() ,
,
故右边抛物线的解析式为y=![]() (x-3)2.
(x-3)2.
故答案为:y=![]() (x-3)2.
(x-3)2.

练习册系列答案
相关题目