题目内容
如图1,AB是⊙O的直径,直线l交⊙O于C1、C2,AD⊥l,垂足为D.(1)求证:AC1•AC2=AB•AD.
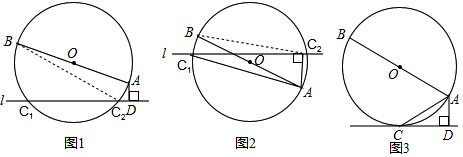
(2)若将直线l向上平移(如图2),交⊙O于C1、C2,使弦C1C2与直径AB相交(交点不与A、B重合),其他条件不变,请你猜想,AC1、AC2、AB、AD之间的关系,并说明理由.
(3)若将直线l平移到与⊙O相切时,切点为C,其他条件不变,请你在图3上画出变化后的图形,标好相应的字母并猜想AC、AB、AD的关系是什么?(只写出关系,不加以说明)
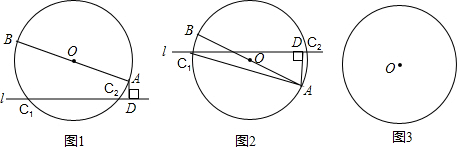
分析:(1)本题要通过构建相似三角形来求解.连接AC1、BC2,通过证△ABC2∽△AC1D可得出所求结论.(所证的两个三角形中,同弧对的圆周角相等以及一组直角);
(2)结论同(1)也是通过证△ABC2∽△AC1D来得出所求结论;
(3)当直线l与圆相切时,C1、C2重合,因此结论变为AC2=AB•AD,可通过证三角形ABC和ACD相似,通过弦切角和一组直角来证得两三角形相似.
(2)结论同(1)也是通过证△ABC2∽△AC1D来得出所求结论;
(3)当直线l与圆相切时,C1、C2重合,因此结论变为AC2=AB•AD,可通过证三角形ABC和ACD相似,通过弦切角和一组直角来证得两三角形相似.
解答:(1)证明:连接BC2.
∵AB为直径,∴∠BC2A=90度.
∵AD⊥l,即∠ADC1=90°,
∴∠BC2A=∠ADC1.
又∵∠B=∠AC1D,
∴△ABC2∽△AC1D.
∴
=
.
∴AC1•AC2=AB•AD.
(2)解:当l向上平移后,连接BC2.
∵AB为直径,
∴∠BC2A=90度.
∵AD⊥l,即∠ADC1=90°,
∴∠BC2A=∠ADC1.
又∵∠B=∠AC1D,
∴△ABC2∽△AC1D.
∴
=
.
∴AC1•AC2=AB•AD.
(3)解:AC2=AB•AD.
画草图.
∵AB为直径,∴∠BC2A=90度.
∵AD⊥l,即∠ADC1=90°,
∴∠BC2A=∠ADC1.
又∵∠B=∠AC1D,
∴△ABC2∽△AC1D.
∴
| AC2 |
| AD |
| AB |
| AC1 |
∴AC1•AC2=AB•AD.
(2)解:当l向上平移后,连接BC2.
∵AB为直径,
∴∠BC2A=90度.
∵AD⊥l,即∠ADC1=90°,
∴∠BC2A=∠ADC1.
又∵∠B=∠AC1D,
∴△ABC2∽△AC1D.
∴
| AC2 |
| AD |
| AB |
| AC1 |
∴AC1•AC2=AB•AD.
(3)解:AC2=AB•AD.
画草图.

点评:本题主要考查了圆周角定理和相似三角形的判定和性质.根据相似三角形来求线段成比例是解题的基本思路.

练习册系列答案
相关题目

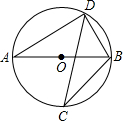 如图,若AB是⊙0的直径,CD是⊙O的弦,∠C=30°,BD=1,则⊙O的半径是( )
如图,若AB是⊙0的直径,CD是⊙O的弦,∠C=30°,BD=1,则⊙O的半径是( ) (2013•海沧区一模)如图,若AB是⊙O的直径,CD是⊙O的弦,∠ABD=50°,则∠BCD=
(2013•海沧区一模)如图,若AB是⊙O的直径,CD是⊙O的弦,∠ABD=50°,则∠BCD=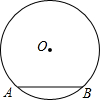 如图,弦AB是⊙O的内接正方形的一条边,则弦AB所对的圆周角的度数为
如图,弦AB是⊙O的内接正方形的一条边,则弦AB所对的圆周角的度数为