题目内容
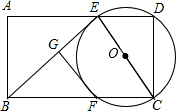 如图,矩形ABCD中,AB=3,AD=5.点E是AD上的动点,以CE为直径的⊙O与BC交于点F,过点F作FG⊥BE于点G.
如图,矩形ABCD中,AB=3,AD=5.点E是AD上的动点,以CE为直径的⊙O与BC交于点F,过点F作FG⊥BE于点G.
(1)若FG是⊙O的切线,求DE的长度;
(2)试探究:BE能否与⊙O相切?若能,求出此时DE的长度;若不能,请说明理由.
解:(1)连接EF,FD;
∵GF为圆的切线且又和EB垂直,
∴BE∥FD,
∴∠BEF=∠DFE;
又∵∠DFE=∠FEC,
∴∠BEF=∠CEF,
∴EF为∠BEC的平分线;
∵∠EFC=90°,
∴EF⊥BC,
∴BE=CE
∴△BEC为等腰三角形,
∴BF为BC的一半;
∵ED∥BF,
∴四边形BEDF为平行四边形,
即ED=BF=2.5;
(2)BE不能与⊙O相切.
∵若BE与圆相切,
∴BE⊥EC;
∴△BEC是圆内接三角形,即BC为直径,EF为一个半径,
∵最短为3>2.5,
∴BE不能与⊙O相切.
分析:(1)连接EF,FD,由GF为圆的切线且又和EB垂直,可知BE∥FD,推出∠BEF=∠DFE,而∠DFE=∠FEC可得∠BEF=∠CEF所以EF为∠BEC的平分线.又因为∠EFC为直角可知EF⊥BC,所以△BEC为等腰三角形,得到BF为BC的一半,又因为ED∥BF,可知四边形BEDF为平行四边形,即ED=BF=2.5.
(2)若BE与圆相切,BE必垂直EC,我们可把三角形BEC看作一个圆内接三角形,即BC为直径,EF为一个半径,但最短为3>2.5,所以BE不能与⊙O相切.
点评:本题考查了圆内接图形和切线的性质,做题时注意巧妙运用辅助线.
∵GF为圆的切线且又和EB垂直,
∴BE∥FD,
∴∠BEF=∠DFE;
又∵∠DFE=∠FEC,
∴∠BEF=∠CEF,
∴EF为∠BEC的平分线;
∵∠EFC=90°,
∴EF⊥BC,
∴BE=CE
∴△BEC为等腰三角形,
∴BF为BC的一半;
∵ED∥BF,
∴四边形BEDF为平行四边形,
即ED=BF=2.5;

(2)BE不能与⊙O相切.
∵若BE与圆相切,
∴BE⊥EC;
∴△BEC是圆内接三角形,即BC为直径,EF为一个半径,
∵最短为3>2.5,
∴BE不能与⊙O相切.
分析:(1)连接EF,FD,由GF为圆的切线且又和EB垂直,可知BE∥FD,推出∠BEF=∠DFE,而∠DFE=∠FEC可得∠BEF=∠CEF所以EF为∠BEC的平分线.又因为∠EFC为直角可知EF⊥BC,所以△BEC为等腰三角形,得到BF为BC的一半,又因为ED∥BF,可知四边形BEDF为平行四边形,即ED=BF=2.5.
(2)若BE与圆相切,BE必垂直EC,我们可把三角形BEC看作一个圆内接三角形,即BC为直径,EF为一个半径,但最短为3>2.5,所以BE不能与⊙O相切.
点评:本题考查了圆内接图形和切线的性质,做题时注意巧妙运用辅助线.

练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
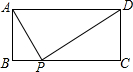 如图,矩形ABCD中,AD=a,AB=b,要使BC边上至少存在一点P,使△ABP、△APD、△CDP两两相似,则a、b间的关系式一定满足( )
如图,矩形ABCD中,AD=a,AB=b,要使BC边上至少存在一点P,使△ABP、△APD、△CDP两两相似,则a、b间的关系式一定满足( )A、a≥
| ||
| B、a≥b | ||
C、a≥
| ||
| D、a≥2b |
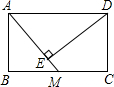 如图,矩形ABCD中,AB=6,BC=8,M是BC的中点,DE⊥AM,E是垂足,则△ABM的面积为
如图,矩形ABCD中,AB=6,BC=8,M是BC的中点,DE⊥AM,E是垂足,则△ABM的面积为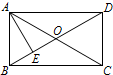 7、如图,矩形ABCD中,AE⊥BD,垂足为E,∠DAE=2∠BAE,则∠CAE=
7、如图,矩形ABCD中,AE⊥BD,垂足为E,∠DAE=2∠BAE,则∠CAE= (2008•怀柔区二模)已知如图,矩形ABCD中,AB=3cm,BC=4cm,E是边AD上一点,且BE=ED,P是对角线上任意一点,PF⊥BE,PG⊥AD,垂足分别为F、G.则PF+PG的长为
(2008•怀柔区二模)已知如图,矩形ABCD中,AB=3cm,BC=4cm,E是边AD上一点,且BE=ED,P是对角线上任意一点,PF⊥BE,PG⊥AD,垂足分别为F、G.则PF+PG的长为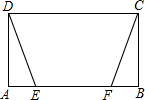 (2002•西藏)已知:如图,矩形ABCD中,E、F是AB边上两点,且AF=BE,连结DE、CF得到梯形EFCD.
(2002•西藏)已知:如图,矩形ABCD中,E、F是AB边上两点,且AF=BE,连结DE、CF得到梯形EFCD.