题目内容
【题目】如图,已知直线c和a、b分别交于A、B两点,点P在直线c上运动.
(1)若P点在AB两点之间运动,试探究:当∠1、∠2和∠3之间满足什么数量关系时,a∥b?
(2)若P点在AB两点外侧运动,试探究:当∠1、∠2和∠3之间满足什么数量关系时,a∥b?(直接写出结论即可)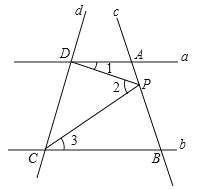
【答案】解:(1)∠1+∠3=∠2时,a∥b;
过P作MP∥a,
∵MP∥a,
∴∠1=∠DPM,
∵∠1+∠3=∠2,
∴∠3=∠MPC,
∴MP∥BC,
∴a∥b;
(2)若P点在A点上部运动时,∠3﹣∠1=∠2时,a∥b;
若P点在B点下部运动时,∠1﹣∠3=∠2时,a∥b.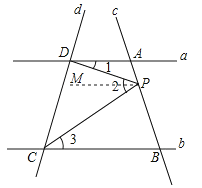
【解析】(1)过P作MP∥a,根据平行线的性质可得∠1=∠DPM,然后可得∠3=∠MPC,进而得到MP∥BC,再根据平行线的传递性可得a∥b;
(2)若P点在AB两点外侧运动,∠1﹣∠3=∠2时,a∥b,证明方法与(1)相同.
【考点精析】解答此题的关键在于理解平行线的判定的相关知识,掌握同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行.

练习册系列答案
相关题目