ЬтФПФкШн
ЁОЬтФПЁПзїЭМВЂЬюПе
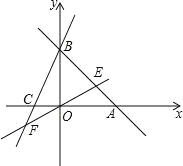
ШчЭМЃЌдкRtЁїABCЃЌЁЯBACЃН90ЁуЃЌADЁЭBCгкDЃЌдкЂкЂлЭМжаЃЌMNЃНABЃЌЁЯMNEЃНЁЯBЃЌЯжвЊвдЂкЂлЭМЮЊЛљДЁЃЌдкЩфЯпNEЩЯШЗЖЈвЛЕуPЃЌЙЙдьГівЛИіЁїMNPгыЂйЭМжаФГвЛИіШ§НЧаЮШЋЕШ.
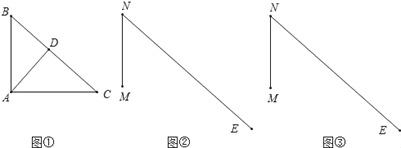
(1)гУБпГЄЯожЦPЕуЃЌЛЗЈЃК_____ЃЌПЩИљОнSASЃЌAASЃЌASAЃЌHLжаЕФ______ЕУЕН______ЃЎ
(2)гУжБНЧЯожЦЕуPЃЌЛЗЈЃК_______ЃЌПЩИљОнSASЃЌAASЃЌASAЃЌHLжаЕФ______ЕУЕН______ЃЎ
ЁОД№АИЁП(1)зїNPЃНBCЃЛSASЃЛЁїMNPЁеЁїABCЃЛ(2)Й§MзїMCЁЭMNЃЛASAЃЛЁїMNPЁеЁїABCЃЎ
ЁОНтЮіЁП
(1)зїNP=BC,МДПЩжЄУїЁїMNPЁеЁїABC,МДПЩНтЬт;
(2)Й§MзїMCЁЭMN,ПЩжЄУїЁїMNPЁеЁїABC,ПЩЕУД№АИ.
жЄУїЃК(1)зїNPЃНBCЃЌ
ЁпдкЁїMNPКЭЁїABCжаЃЌ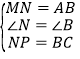 ЃЌ
ЃЌ
ЁрЁїMNPЁеЁїABCЃЌ(SAS)
(2)Й§MзїMCЁЭMNЃЌ
ЁпдкЁїMNPКЭЁїABCжаЃЌ ЃЌ
ЃЌ
ЁрЁїMNPЁеЁїABCЃЌ(ASA)
ЙЪД№АИЮЊЃКNPЃНBCЃЛSASЃЛЁїMNPЁеЁїABCЃЛЙ§MзїMCЁЭMNЃЛASAЃЛЁїMNPЁеЁїABCЃЎ

 ОйвЛЗДШ§ЭЌВНЧЩНВОЋСЗЯЕСаД№АИ
ОйвЛЗДШ§ЭЌВНЧЩНВОЋСЗЯЕСаД№АИ ПкЫугыгІгУЬтПЈЯЕСаД№АИ
ПкЫугыгІгУЬтПЈЯЕСаД№АИ УћЪІЕуОІзжДЪОфЖЮЦЊЯЕСаД№АИ
УћЪІЕуОІзжДЪОфЖЮЦЊЯЕСаД№АИЁОЬтФПЁПааЪЛжаЕФЦћГЕЃЌдкЩВГЕКѓгЩгкЙпадЕФдвђЃЌЛЙвЊМЬајЯђЧАЛЌаавЛЖЮОрРыВХФмЭЃзЁЃЌетЖЮОрРыГЦЮЊЁАЩВГЕОрРыЁБЃЎЮЊСЫВтЖЈФГжжаЭКХЦћГЕЕФЩВГЕадФмЃЌЖдетжжЦћГЕЕФЩВГЕОрРыНјааВтЪдЃЌВтЕУЕФЪ§ОнШчЯТБэЃК
ЩВГЕЪБГЕЫй(ЧЇУз/ЪБ) | 0 | 5 | 10 | 15 | 20 | 25 | 30 |
ЩВГЕОрРы(Уз) | 0 | 0.1 | 0.3 | 0.6 | 1 | 1.6 | 2.1 |
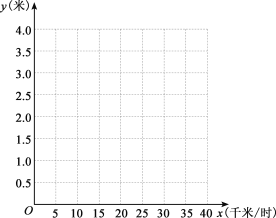
ЃЈ1ЃЉдкШчЭМЫљЪОЕФжБНЧзјБъЯЕжаЃЌвдЩВГЕЪБГЕЫйЮЊКсзјБъЃЌвдЩВГЕОрРыЮЊзнзјБъЃЌУшГіетаЉЪ§ОнЫљБэЪОЕФЕуЃЌВЂгУЦНЛЌЕФЧњЯпСЌНсетаЉЕуЃЌЕУЕНФГКЏЪ§ЕФДѓжТЭМЯѓЃЛ
ЃЈ2ЃЉВтСПБиШЛДцдкЮѓВюЃЌЭЈЙ§ЙлВьЭМЯѓЙРМЦКЏЪ§ЕФРраЭЃЌЧѓГівЛИіДѓжТТњзуетаЉЪ§ОнЕФКЏЪ§БэДяЪНЃЛ
ЃЈ3ЃЉвЛСОИУаЭКХЦћГЕдкИпЫйЙЋТЗЩЯЗЂЩњНЛЭЈЪТЙЪЃЌЯжГЁВтЕУЩВГЕОрРыдМЮЊ40УзЃЌвбжЊетЬѕИпЫйЙЋТЗЯоЫй100ЧЇУз/ЪБЃЌЧыИљОнФуШЗЖЈЕФКЏЪ§БэДяЪНЃЌЭЈЙ§МЦЫуХаЖЯдкЪТЙЪЗЂЩњЪБЃЌЦћГЕЪЧЗёГЌЫйааЪЛЃЎ