题目内容
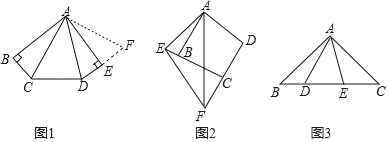
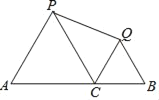
【题目】如图，AB＝12，C是线段AB上一点，分别以AC、CB为边在A的同侧作等边△ACP和等边△CBQ，连接PQ，则PQ的最小值是（ ）
A. 3B. 4C. 5D. 6
【答案】D
【解析】
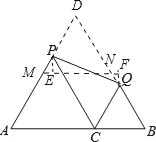
分别延长AP、BQ交于点D，易证四边形CPDQ为平行四边形，得出PD+DQ＝PC+CQ＝AC+BC＝12，作△ABD的中位线MN，则MD＝DN＝MN＝
AB，运用中位线的性质和等边三角形的性质求出MD＝DN＝MN＝AB，进而求得MD+DN＝PD+DQ，得出PM＝QN，作PE⊥MN，QF⊥MN，则PE∥QF，然后证得△PME≌△QNF，从而证得MN＝EF，根据平行线间的距离得出PQ≥EF，从而求得PQ的最小值．
解：如图，分别延长AP、BQ交于点D，
∵∠A＝∠QCB＝60°，
∴AD∥CQ，
∵∠B＝CPCA＝60°，
∴BD∥PC，
∴四边形CPDQ为平行四边形，
∴PD＝CQ，PC＝DQ，
∴PD+DQ＝PC+CQ＝AC+BC＝12，
作△ABD的中位线MN，则MD＝DN＝MN＝AB，
∴MD+DN＝AB＝12，
∴MD+DN＝PD+DQ，
∴PM＝QN，
作PE⊥MN，QF⊥MN，
∴PE∥QF，
∴∠PEM＝∠QFN＝90°，且∠PME＝∠QNF＝60°，PM＝QN
∴△PME≌△QNF（AAS），
∴EM＝FN，
∴MN＝EF，
∴PQ≥EF，
∴C是线段AB的中点时，PQ的值最小，最小值为AB＝6．
故选：D．
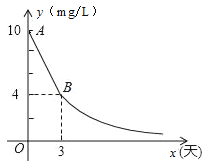
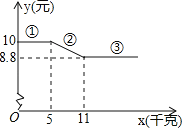
【题目】环保局对某企业排污情况进行检测，结果显示：所排污水中硫化物的浓度超标，即硫化物的浓度超过最高允许的1.0 mg/L．环保局要求该企业立即整改，在15天以内（含15天）排污达标．整改过程中，所排污水中硫化物的浓度y（mg/L）与时间x（天）的变化规律如图所示，其中线段AB表示前3天的变化规律，其中第3天时硫化物的浓度降为4 mg/L．从第3天起所排污水中硫化物的浓度y与时间x满足下面表格中的关系：
时间x（天） | 3 | 4 | 5 | 6 | 8 | …… |
硫化物的浓y（mg/L） | 4 | 3 | 2.4 | 2 | 1.5 |
（1）求整改过程中当0≤x<3时，硫化物的浓度y与时间x的函数表达式；
（2）求整改过程中当x≥3时，硫化物的浓度y与时间x的函数表达式；
（3）该企业所排污水中硫化物的浓度，能否在15天以内不超过最高允许的1.0 mg/L？为什么？
