题目内容
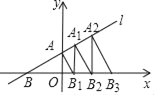
【题目】在正方形网格中,每个小正方形的边长都是1个单位长度,△ABC在平面直角坐标系中的位置如图所示.
(1)作出将△ABC向右平移 2个单位长度后得到的△A1B1C1;
(2)作出将△ABC绕点O顺时针旋转90°后得到的△A2B2C2;
(3)求在(2)的旋转变换中,线段BC扫过区域的面积(结果保留π)

【答案】(1)(2)如图见解析;(3)3π.
【解析】
(1)利用网格特点和平移的性质画出点A、B、C的对应点A1、B1、C1,从而得到△A1B1C1;
(2)利用网格特点和旋转的性质画出点A1、B1、C1的对应点A2、B2、C2,从而得到△A2B2C2;
(3)根据扇形的面积公式,利用线段BC扫过区域的面积=S扇形COC2-S扇形BOB2进行计算即可.
(1)如图,△A1B1C1为所作;
(2)如图,△A2B2C2为所作;
(3)线段BC扫过区域的面积=S扇形COC2﹣S扇形BOB2=![]() ﹣
﹣![]() =3π.
=3π.

练习册系列答案
相关题目