题目内容
【题目】已知:在四边形ABCD中,AB=AD,∠ABC+∠ADC=180°
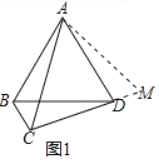
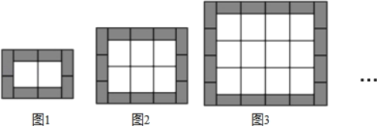
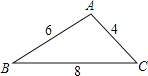
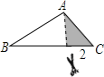
(1)如图①,若∠ACD=60°,BC=1,CD=3,则AC的长为 ;
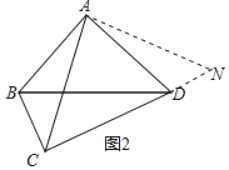
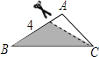
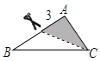
(2)如图②,若∠ACD=45°,BC=1,CD=3,求出AC的长;
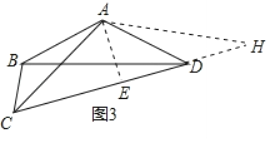
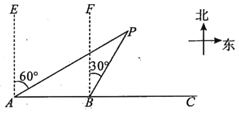
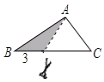
(3)如图③,若∠ACD=30°,BC=a,CD=b,直接写出AC的长.

【答案】(1)4;(2)AC=2![]() ;(3)AC=
;(3)AC=![]() (a+b).
(a+b).
【解析】
(1)延长CD至M,使DM=BC,连接AM,证明△ABC≌△ADM,可得△ACM为等边三角形,等量代换可得AC=CM=CD+DM=CD+BC=4;
(2)延长CD至N,使DN=BC,连接AN,证明△ABC≌△ADN,△ACN为等腰直角三角形,可得AC=![]() (CD+BC)=2
(CD+BC)=2![]() ;
;
(3)延长CD至H,使DH=BC,连接AH,作AE⊥CD于E,由(2)可知,AC=AH,
CE=![]() (a+b),在Rt△ACE中可求出AC=
(a+b),在Rt△ACE中可求出AC=![]() (a+b).
(a+b).
解:(1)延长CD至M,使DM=BC,连接AM,
∵∠ABC+∠ADC=180°,∠ADM+∠ADC=180°,
∴∠ABC=∠ADM,
在△ABC和△ADM中,
 ,
,
∴△ABC≌△ADM(SAS)
∴AM=AC,
∵∠ACD=60°,AM=AC,
∴△ACM为等边三角形,
∴AC=CM=CD+DM=CD+BC=4,
故答案为:4;
(2)延长CD至N,使DN=BC,连接AN,
∵∠ABC+∠ADC=180°,∠ADN+∠ADC=180°,
∴∠ABC=∠ADN,
由(1)得,△ABC≌△ADN,
∴AN=AC,
∵∠ACD=45°,AN=AC,
∴△ACN为等腰直角三角形,
∴AC=![]() (CD+BC)=2
(CD+BC)=2![]() ;
;
(3)延长CD至H,使DH=BC,连接AH,作AE⊥CD于E,
由(2)可知,AC=AH,
∴CE=![]() (a+b),
(a+b),
在Rt△ACE中,∠AEC=90°,∠ACD=30°,
∴CE=![]() AC,
AC,
∴AC=![]() (a+b)×
(a+b)×![]() =
=![]() (a+b).
(a+b).