Question

如图，梯形ABCD中，AD∥BC，∠ABC=90°，AD=9，BC=12，AB=a，在线段BC上任取一点P，连接DP，作射线PE⊥DP，PE与直线AB交于点E．
（1）试确定CP=3，点E的位置；
（2）若设CP=x，BE=y，试写出y关于自变量x的函数关系式；
（3）若在线段BC上能找到不同的两点P₁，P₂使按上述作法得到的点E都与点A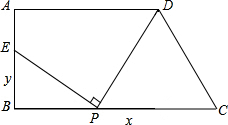重合，试求出此时a的取值范围．

Answer 1

分析：（1）当CP=3时，易知四边形ADPB是矩形，由DP⊥BC，PE⊥DP，得出点E与点B重合；
（2）作DF⊥BC，F为垂足．欲求y关于自变量x的函数关系式，分为两种情况点P在BF上，点P在CF上，通过证明Rt△PEB∽Rt△DPF分别得出；
（3）点E与点A重合，求出此时a的取值范围，可由（2）得出函数关系式，根据题意及根的判别式得出．

解答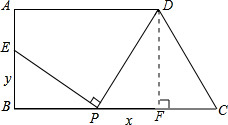：解：（1）作DF⊥BC，F为垂足．
当CP=3时，
∵四边形ADP（F）B是矩形，则CF=3，
∴点P与F重合．
又BF⊥FD，
∴此时点E与点B重合；（2分）

（2）当点P在BF上时，
因而Rt△PEB∽Rt△DPF
∴

BE

BP

=

FP

FD

①
y=-

(12-x)(x-3)

a

=-

(x2-15x+36)

a

②
当点P在CF上时，同理可求得y=

(x2-15x+36)

a

；（6分）

（3）当点E与A重合时，y=EB=a，此时点P在线段BF上，
由②得，a=

(x2-15x+36)

a

，
整理得，x²-15x+36-a²=0 ③
由于在线段BC上能找到两个不同的点P₁与P₂满足条件，也就是说方程③有两个不相等的正根（8分）
故有△=（-15）²-4×（36-a²）＞0．
解得：a²＜

81

4

，
又∵a＞0，
∴0＜a＜

9

2

．（只写a＜

9

2

不扣分）（10分）

点评：本题数形结合，综合考查了直角梯形的性质，相似三角形的性质与函数的关系，函数中根的判别式的应用．