题目内容
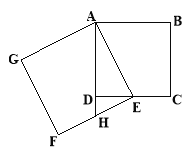
【题目】如图,正方形AEFG的顶点E在正方形ABCD的边CD上;AD的延长线交EF于H点.
(1)试说明:△AED∽△EHD
(2)若E为CD的中点,求![]() 的值.
的值.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
试题(1)根据正方形性质得出∠ADE=∠HDE=90°,∠AEH=90°,求出∠DAE=∠DEH,根据相似三角形的判定推出即可;
(2)根据相似得出比例式![]() ,即可求出答案.
,即可求出答案.
试题解析:(1)∵四边形ABCD是正方形,
∴AD=DC,∠ADE=∠HDE=90°,
∵四边形AEFG是正方形,
∴∠AEH=90°,
∴∠DAE+∠AED=90°,∠AED+∠DEH=90°,
∴∠DAE=∠DEH,
∵∠ADE=∠HDE=90°,
∴△AED∽△EHD;
(2)∵△AED∽△EHD,
∴![]() ,
,
∵E为CD的中点,
∴DC=2DE,
∴AD=2DE,
∴![]() ,
,
∴![]() .
.

练习册系列答案
相关题目
【题目】为让家园更美丽,我市今年进一步推进全国文明城市、 国家卫生城市的创建工作,学校把“双创”工作推向深入,组织了以文明卫生知识竞赛,每班派相同人数的学生参加,成绩分别为![]() 四个等级.其中相应等级的得分依次记为
四个等级.其中相应等级的得分依次记为![]() 分、
分、![]() 分、
分、![]() 分、
分、![]() 分,学校将八年级的一班和二班的成绩整理并绘制成如下统计图表:
分,学校将八年级的一班和二班的成绩整理并绘制成如下统计图表: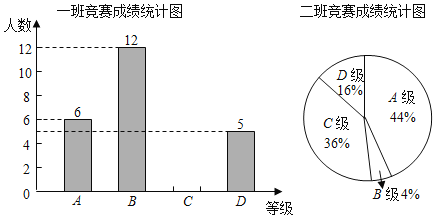
班级 | 平均数(分) | 中位数(分) | 众数(分) |
一班 |
|
|
|
二班 |
|
|
|
根据以上提供的信息解答下列问题:
(1)请补全一班竞赛成绩统计图;
(2)请直接写出![]() 的值;
的值;
(3)你认为哪个班成绩较好,诸写出支持你观点的理由.