题目内容
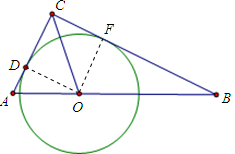
如图,在△ABC中,∠C=90°,AC+BC=8,∠ACB的平分线交AB于点O,以O为 圆心的⊙O与AC相切于点D.
圆心的⊙O与AC相切于点D.
(1)求证:⊙0与BC相切;
(2)当AC=2时,求⊙O的半径.
 圆心的⊙O与AC相切于点D.
圆心的⊙O与AC相切于点D.(1)求证:⊙0与BC相切;
(2)当AC=2时,求⊙O的半径.
(1)过点O作OF⊥BC,垂直为F,连接OD,
∵AC是圆的切线,
∴OD⊥AC,
又OC为∠ACB的平分线,
∴OF=OD,
∴BC与⊙0相切;
(2)由(1)知BC与⊙0相切,
∵D、F为切点,
∴OD⊥AC,OF⊥BC,OD=OF,
S△ABC=S△AOC+S△BOC
=
AC•BC=
AC•OD+
BC•OF
∵AC+BC=8,AC=2,
∴BC=6,
∴
×2×6=
×2×OD+
×6×OF,
而OD=OF.
∴OD=
,
即⊙O的半径为
.
∵AC是圆的切线,
∴OD⊥AC,
又OC为∠ACB的平分线,
∴OF=OD,
∴BC与⊙0相切;
(2)由(1)知BC与⊙0相切,
∵D、F为切点,
∴OD⊥AC,OF⊥BC,OD=OF,
S△ABC=S△AOC+S△BOC
=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∵AC+BC=8,AC=2,
∴BC=6,
∴
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
而OD=OF.
∴OD=
| 3 |
| 2 |
即⊙O的半径为
| 3 |
| 2 |


练习册系列答案
相关题目



 BM于N,AN的延长线交BC于D,直线AB交⊙A于P,K两点,作MT⊥BC于T.
BM于N,AN的延长线交BC于D,直线AB交⊙A于P,K两点,作MT⊥BC于T. =PB,连接AO、BO、AB,并延长BO与切线PA相交于点Q.
=PB,连接AO、BO、AB,并延长BO与切线PA相交于点Q.
