Question

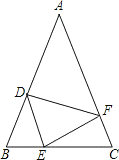
【题目】如图，在△ABC中，AB=AC，点D，E，F分别在AB，BC，AC边上，且BE=CF，BD=CE．

（1）求证：DE=EF；

（2）当∠A=44°时，求∠DEF的度数；

（3）当∠A等于多少度时，△DEF成为等边三角形？试证明你的结论．

Answer 1

【答案】（1）见解析（2）∠DEF=68°；（3）当∠A等于60度时，△DEF成为等边三角形，见解析.

【解析】

（1）根据AB=AC可得∠B=∠C，即可求证△BDE≌△CEF，即可解题；

（2）根据全等三角形的性质，得出∠BED=∠CFE，再根据三角形内角和定理以及平角的定义，即可求得∠DEF的度数；

（3）根据△DEF为等边三角形，以及△BDE≌△CEF，可得∠C的度数，最后根据等腰三角形ABC，求得其顶角的度数．

解：（1）∵AB=AC，

∴∠B=∠C，

∵在△BDE和△CEF中，

，

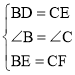∴△BDE≌△CEF（SAS），

∴DE=EF；

（2）当∠A=44°时，∠B=∠C=（180°﹣44°）=68°，

∵△BDE≌△CEF，

∴∠BED=∠CFE，

∵△CEF中，∠CEF+∠CFE=180°﹣68°=112°，

∴∠BED+∠CEF=112°，

∴∠DEF=180°﹣112°=68°；

（3）当∠A等于60度时，△DEF成为等边三角形．

证明：若△DEF为等边三角形，则∠DEF=60°，

∴∠BED+∠CEF=120°，

又∵△BDE≌△CEF，

∴∠BED=∠CFE，

∴△CEF中，∠CEF+∠CFE=120°，

∴∠C=180°﹣120°=60°=∠B，

∴△ABC中，∠A=180°﹣60°×2=60°．