题目内容
(2013•泉州模拟)已知ab=2.①若-1≤
≤-
,则a的取值范围是
| 1 |
| b |
| 1 |
| 3 |
-2≤a≤-
| 2 |
| 3 |
-2≤a≤-
;②若b>0,且a2+b2=5,则a+b=| 2 |
| 3 |
3
3
.分析:①利用不等式的性质由ab=2得到
=
,再代入-1≤
≤-
得a的不等式组,然后解不等式组即可;
②根据完全平方公式得到(a+b)2=a2+2ab+b2,再把ab=2,a2+b2=5得(a+b)2=9,由于b>0,则a>0,利用算术平方根的定义即可得到a+b的值.
| 1 |
| b |
| a |
| 2 |
| 1 |
| b |
| 1 |
| 3 |
②根据完全平方公式得到(a+b)2=a2+2ab+b2,再把ab=2,a2+b2=5得(a+b)2=9,由于b>0,则a>0,利用算术平方根的定义即可得到a+b的值.
解答:解:①∵ab=2,
∴
=
,
而-1≤
≤-
,
∴-1≤
≤-
,
∴-2≤a≤-
;
②∵(a+b)2=a2+2ab+b2,
而ab=2,a2+b2=5,
∴(a+b)2=5+2×2=9,
∵b>0,
∴a>0,
∴a+b=
=3.
故答案为-2≤a≤-
;3.
∴
| 1 |
| b |
| a |
| 2 |
而-1≤
| 1 |
| b |
| 1 |
| 3 |
∴-1≤
| a |
| 2 |
| 1 |
| 3 |
∴-2≤a≤-
| 2 |
| 3 |
②∵(a+b)2=a2+2ab+b2,
而ab=2,a2+b2=5,
∴(a+b)2=5+2×2=9,
∵b>0,
∴a>0,
∴a+b=
| 9 |
故答案为-2≤a≤-
| 2 |
| 3 |
点评:本题考查了完全平方公式:a2±2ab+b2=(a±b)2.也考查了不等式的性质.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
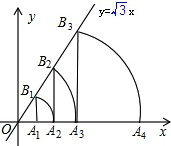 (2013•泉州模拟)如图,直线
(2013•泉州模拟)如图,直线 (2013•泉州模拟)如图所示,课外活动中,小明在与旗杆AB距离为10米的C处,用测角仪测得旗杆顶部A的仰角为45°.已知测角仪器的高CD=1.5米,则旗杆AB的高是
(2013•泉州模拟)如图所示,课外活动中,小明在与旗杆AB距离为10米的C处,用测角仪测得旗杆顶部A的仰角为45°.已知测角仪器的高CD=1.5米,则旗杆AB的高是