题目内容
已知一次函数y=kx+b的图象与反比例函数 的图象相交于点P(2,1),与x轴交于点E,与y轴交于点F,O为坐标原点.
的图象相交于点P(2,1),与x轴交于点E,与y轴交于点F,O为坐标原点.
(1)求k,b的值;
(2)在同一坐标系中画出这两个函数的图象;
(3)△EOF的面积是△EOP的面积的多少倍?
(4)能不能在反比例函数 的图象上找到一点Q,使△QOE的面积△EOF的面积相等?如果能,请写出Q点的坐标;若不能,请说明理由.
的图象上找到一点Q,使△QOE的面积△EOF的面积相等?如果能,请写出Q点的坐标;若不能,请说明理由.
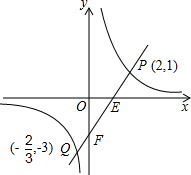 (1)∵点P(2,1)在反比例函数
(1)∵点P(2,1)在反比例函数 的图象上,
的图象上,∴1=
 ,
,解得:k=2,
∵点P(2,1)在一次函数y=kx+b的图象上,
∴1=2×2+b,
解得:b=-3,
∴k=2,b=-3;
(2)图象如右图:
(3)∵E(
 ,0),F(0,-3),
,0),F(0,-3),∴S△EOF=
 ×OE×OF=
×OE×OF= ×
× ×3=
×3= ,
,S△EOP=
 ×
× ×1=
×1= ,
,∴S△EOF=3S△EOP;
(4)能.理由如下:
若S△QOE=S△EOF,
则Q的纵坐标为±3,
令y=±3,代入
 ,得
,得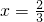 .
.∴Q(
 ,3)或Q(-
,3)或Q(- ,-3).
,-3).分析:(1)将点P代入反比例函数
 求得k值,再代入一次函数求得b值;
求得k值,再代入一次函数求得b值;(2)根据求得的函数画出函数图象;
(3)由于OE边相同,则
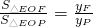 ;
;(4)设出Q点坐标,由△QOE的面积△EOF的面积相等,求出Q点坐标.
点评:本题考查了反比例函数
 中k的几何意义,即过双曲线上任意一点引x轴、y轴垂线,所得矩形面积为|k|,是经常考查的一个知识点.
中k的几何意义,即过双曲线上任意一点引x轴、y轴垂线,所得矩形面积为|k|,是经常考查的一个知识点. 
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 已知一次函数y=kx+2的图象经过A(-1,1).
已知一次函数y=kx+2的图象经过A(-1,1). m≠0)的图象相交于点 A(1,3)、B(n,-1)两点.
m≠0)的图象相交于点 A(1,3)、B(n,-1)两点.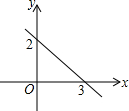 已知一次函数y=kx+b的图象如图所示,指出k、b的符号,并求出k和b的值.
已知一次函数y=kx+b的图象如图所示,指出k、b的符号,并求出k和b的值.