题目内容
阅读材料：
为解方程（x-1）2-5（x-1）+4=0时，我们可以将x-1看作一个整体，然后设x-1=y…．①，那么原方程可化为y2-5y+4=0，解得y1=1，y2=4．当y=1时，x-1=1，∴x=2；当y=4时，x-1=4，∴x=5；故原方程的解为x1=2，x2=5．
解答问题：
（1）上述解题过程，在由原方程得到方程①的过程中，运用了______法达到了解方程的目的，体现了转化的数学思想；
（2）请利用以上知识解方程：（3x+5）2-4（3x+5）+3=0．
解：（1）∵将x-1看作一个整体，然后设x-1=y，实际上是将x-1转化为了y，
∴这一步是运用了数学里的转化思想，这种方法交换元法．
答案为：换元．
（2）设3x+5=y，则原方程变形为：
y2-4y+3=0，
解得：y1=1，y2=3．
当y=1时，
3x+5=1，
x=-
；
当y=3时，
3x+5=3，
x=-
，
∴x1=
，x2=-．
分析：（1）根据题目的变形可以看出运用了换元法和整体思想在解答这道题，故得出结论为换元法．
（2）先设3x+5=y，原方程可以变为：y2-4y+3=0，再解一道关于y的方程求出y的值，再分别代入3x+5就可以求出x的值．
点评：本题考查了换元法解一元二次方程的运用，因式分解法解一元二次方程的运用，解答时运用数学整体思想换元是关键．
∴这一步是运用了数学里的转化思想，这种方法交换元法．
答案为：换元．
（2）设3x+5=y，则原方程变形为：
y2-4y+3=0，
解得：y1=1，y2=3．
当y=1时，
3x+5=1，
x=-
；当y=3时，
3x+5=3，
x=-
，∴x1=
，x2=-．分析：（1）根据题目的变形可以看出运用了换元法和整体思想在解答这道题，故得出结论为换元法．
（2）先设3x+5=y，原方程可以变为：y2-4y+3=0，再解一道关于y的方程求出y的值，再分别代入3x+5就可以求出x的值．
点评：本题考查了换元法解一元二次方程的运用，因式分解法解一元二次方程的运用，解答时运用数学整体思想换元是关键．
练习册系列答案
名校课堂系列答案
相关题目
；
，
，
，
，
．
；
，
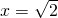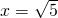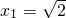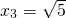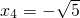，x2=
，x3=
，x4=
．