��Ŀ����
�Ķ����ϣ�Ϊ�ⷽ�̣�x2-1��2-5��x2-1��+4=0�����ǿ��Խ�x2-1����һ�����壬
��x2-1=y���٣�
��ôԭ���̿ɻ�Ϊy2-5y+4=0�����y1=1��y2=4��
��y=1ʱ��x2-1=1����x2=2����x=��
��
��y=4ʱ��x2-1=4����x2=5����x=��
��
��ԭ���̵Ľ�Ϊx1=
��x2=-
��x3=
��x4=-
��
���Ͻ��ⷽ��������Ԫ��������ԭ���̵õ����̢ٵĹ����У����û�Ԫ���ﵽ�˽ⷽ�̵�Ŀ�ģ�������ת������ѧ˼�룻����������֪ʶ�ⷽ�̣�
��1��x4-x2-6=0�� ��2����x2+x��2+��x2+x��=6��
��x2-1=y���٣�
��ôԭ���̿ɻ�Ϊy2-5y+4=0�����y1=1��y2=4��
��y=1ʱ��x2-1=1����x2=2����x=��
| 2 |
��y=4ʱ��x2-1=4����x2=5����x=��
| 5 |
��ԭ���̵Ľ�Ϊx1=
| 2 |
| 2 |
| 5 |
| 5 |
���Ͻ��ⷽ��������Ԫ��������ԭ���̵õ����̢ٵĹ����У����û�Ԫ���ﵽ�˽ⷽ�̵�Ŀ�ģ�������ת������ѧ˼�룻����������֪ʶ�ⷽ�̣�
��1��x4-x2-6=0�� ��2����x2+x��2+��x2+x��=6��
�������Ķ���Ŀ�����塰��Ԫ�����Ľⷨ��Ȼ�����ַ������
����⣺��1��x4-x2-6=0
��x2=y����ԭ���̿ɻ�Ϊ
y2-y-6=0�����y1=3��y2=-2����ȥ����
��y=3ʱ��x2=3����x=��
��ԭ���̵Ľ�Ϊx=��
��
��2����x2+x��2+��x2+x��=6
��x2+x=y����ԭ���̿ɻ�Ϊ
y2+y=6�����y1=-3����ȥ����y2=2��
��y=2ʱ��x2+x=2�����x1=-2��x2=1��
����ԭ���̵Ľ�Ϊx1=-2��x2=1��
��x2=y����ԭ���̿ɻ�Ϊ
y2-y-6=0�����y1=3��y2=-2����ȥ����
��y=3ʱ��x2=3����x=��
| 3 |
��ԭ���̵Ľ�Ϊx=��
| 3 |
��2����x2+x��2+��x2+x��=6
��x2+x=y����ԭ���̿ɻ�Ϊ
y2+y=6�����y1=-3����ȥ����y2=2��
��y=2ʱ��x2+x=2�����x1=-2��x2=1��
����ԭ���̵Ľ�Ϊx1=-2��x2=1��
������������Ҫ�����˻�Ԫ��������ij��ʽ�ӿ���һ�����壬��һ����ĸȥ��������ʵ�е����滻��

��ϰ��ϵ�д�
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
�����Ŀ
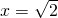 ��
��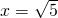 ��
��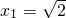 ��
�� ��
��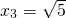 ��
��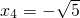 ��
�� ��
�� ��
�� ��x2=
��x2= ��x3=
��x3= ��x4=
��x4= ��
��