题目内容
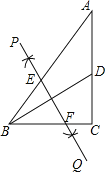
【题目】如图，在Rt△ABC中，∠C=90°，AC=4，BC=3，点D是AC的中点，连接BD，按以下步骤作图：①分别以B，D为圆心，大于
BD的长为半径作弧，两弧相交于点P和点Q；②作直线PQ交AB于点E，交BC于点F，则BF=（ ）
A. 
B. 1C. 
D. 
【答案】C
【解析】
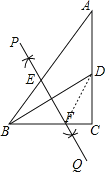
连结DF，利用基本作图得到EF垂直平分BD，则BF=DF，设BF=x，则DF=x，CF=3-x，然后在Rt△DCF中利用勾股定理得到22+（3-x）2=x2，然后解方程即可．
连结DF，由作法得EF垂直平分BD，则BF=DF，
∵点D是AC的中点，
∴CD=
AC=2，
设BF=x，则DF=x，CF=3-x，
在Rt△DCF中，22+（3-x）2=x2，解得x=
，
即BF=．
故选C．
练习册系列答案
相关题目
