题目内容
【题目】如图,△ABC是等边三角形,AD是∠BAC的平分线,△ADE是等边三角形,下列结论:①AD⊥BC;②EF=FD;③BE=BD.其中正确的个数有( )

A.3个 B.2个 C.1个 D.0个
【答案】A
【解析】
试题分析:根据等边三角形性质得出AB=AC,根据三线合一定理得出①正确;求出△BAE≌△CAD,推出BE=DC=BD,∠DAC=∠BAE=30°,求出∠BAE=∠BAD,根据三线合一得出EF=DF.
解:∵△ABC是等边三角形,
∴AB=AC,
∵AD是∠BAC的平分线,
∴AD⊥BC,BD=DC,
∴∠ADC=90°,
∵△ABC和△ADE是等边三角形,
∴AE=AD,AB=AC,∠EAD=∠BAC=60°,
∴∠EAD﹣∠BAD=∠BAC﹣∠BAD,
∴∠BAE=∠DAC,
在△BAE和△CAD中,
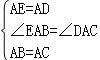 ,
,
∴△BAE≌△CAD(SAS),
∴∠DAC=∠BAE,BE=DC,
∵BD=DC,
∴BE=BD,
∵△ABC是等边三角形,
∴∠BAC=60°,
∵AD是∠BAC的平分线,
∴∠DAC=30°,
∴∠BAE=30°,
∵△ADE是等边三角形,
∴∠DAE=60°,
∴∠BAD=30°=∠BAE,
∵AE=AD,
∴EF=DF(三线合一),
即①②③都正确,
故选A.

练习册系列答案
相关题目
【题目】下表是某水库一周内水位高低的变化情况(用正数记水位比前一日上升数,用负数记下降数).那么本周星期几水位最低( )
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
水位变化/米 | 0.12 | ﹣0.02 | ﹣0.13 | ﹣0.20 | ﹣0.08 | ﹣0.02 | 0.32 |
A. 星期二 B. 星期四 C. 星期六 D. 星期五
