题目内容
【题目】如图，AB为⊙O的直径，CF切⊙O于点C，BF⊥CF于点F，点D在⊙O上，CD交AB于点E，∠BCE=∠BCF．
（1）求证：弧AC=弧AD；
（2）点G在⊙O上，∠GCD=∠FCD，连接DO并延长交CG于点H，求证：CH=GH；
（3）在（2）的条件下，连接AG，AG=3，CF=2
，求CG的长．
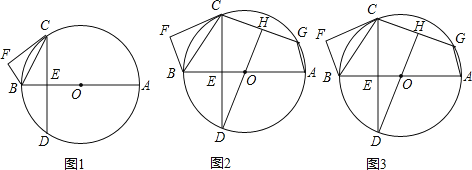
【答案】（1）见解析；（2）见解析；（3）
【解析】
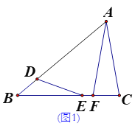
（1）如图1，连接半径，根据切线的性质得出垂直，与已知BF⊥FC，得BF∥OC，所以∠BEC=∠BFC=90°，由垂径定理得：弧AC=弧AD；
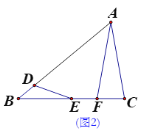
（2）如图2，根据同圆半径相等得∠OCD=∠D，由切线的性质得∠FCD+∠OCD=90°，根据等量代换得：
∠DCG+∠D=90°，所以∠DHC=90°，由垂径定理得CH=HG；
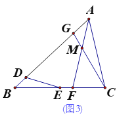
（3）如图3中，延长GA到M，使得AD=AM，连接DM，延长CG到N，使得GN=GD，连接AN，作DJ⊥AM于J．首先证明△CAD≌△MAD，得AM=AC，DM=CD=DG，同理可得GN=DG，AN=AD=AC，再证明DM2-DA2=（DJ2+JM2）-（DJ2+AJ2）=（JM+AJ）（JM-AJ）=AMAG，求出AD，同理可得AN2-AG2=GNCG，延长即可解决问题．
证明：（1）如图1，连接OC，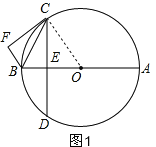
∵OC=OB，
∴∠OBC=∠OCB，
∵FC是⊙O的切线，
∴OC⊥FC，
∵BF⊥FC，
∴BF∥OC，∠BFC=90°，
∴∠OCB=∠FBC，
∴∠OBC=∠FBC，
∵∠BCE=∠BCF，
∴△FBC∽△EBC，
∴∠BEC=∠BFC=90°，
∴OB⊥DC，
∴弧AC=弧AD；
（2）如图2，连接OC．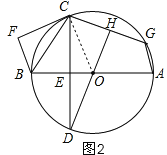
∵OC=OD，
∴∠OCD=∠D，
∵FC是⊙O的切线，
∴∠FCD+∠OCD=90°，
∵∠FCD=∠DCG，
∴∠DCG+∠D=90°，
∴∠DHC=90°，
∴DH⊥CG，
∵DH经过圆心O，
∴CH=HG．
（3）如图3中，延长GA到M，使得AD=AM，连接DM，延长CG到N，使得GN=GD，连接AN，作DJ⊥AM于J．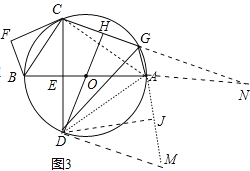
∵CE=CF=2
，
∴CD=2，
∵DC=DG，AC=AD，
∵∠DAM=∠DCG=∠CAD，
∴△CAD≌△MAD，
∴AM=AC，DM=CD=DG，
同理可证GN=DG，AN=AD=AC，
∵DM2-DA2=（DJ2+JM2）-（DJ2+AJ2）=（JM+AJ）（JM-AJ）=AMAG，
∴（4）2-AD2=AD3，
解得AD=13，
同理在等腰三角形△NAC中可得AN2-AG2=GNCG，
∴169-9=4CG，∴CG= ．
