题目内容
在等腰梯形ABCD中,AB=DC=5,AD=4,BC=10.点E在下底边BC上,点F在腰AB上.A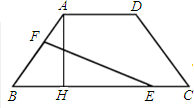 H为等腰梯形的高.
H为等腰梯形的高.(1)求AH的长?
(2)若EF平分等腰梯形ABCD的周长,设BE长为x,试用含x的代数式表示△BEF的面积;
(3)是否存在线段EF将等腰梯形ABCD的周长和面积同时平分?若存在,求出此时BE的长;若不存在,请说明理由;
(4)是否存在线段EF将等腰梯形ABCD的周长和面积同时分成1:2的两部分?若存在,求出此时BE的长;若不存在,请说明理由.
分析:(1)由题意即可推出BH=(BC-AD)÷2,然后根据勾股定理,即可推出高AH的长度;
(2)根据题意画出BE的高FM,然后,推出梯形周长的一半(即12),即可知BF=12-x,通过求证△FBM∽△ABH,即可推出高FM关于x的表达式,最后根据三角形的面积公式,即可表示出△BEF的面积;
(3)通过计算等腰梯形的面积,即可推出其一半的值,然后结合结论(2)即可推出结论;
(4)首先提出假设成立,然后,分情况进行讨论,①若当BE+BF=8,△BEF的面积=
S等腰梯形ABCD=
,根据题意列出方程,求出x;②若当BE+BF=16,△BEF的面积=
S等腰梯形ABCD=
时,根据题意列出方程,求出x,最后即可确定假设不成立,即可推出结论.
(2)根据题意画出BE的高FM,然后,推出梯形周长的一半(即12),即可知BF=12-x,通过求证△FBM∽△ABH,即可推出高FM关于x的表达式,最后根据三角形的面积公式,即可表示出△BEF的面积;
(3)通过计算等腰梯形的面积,即可推出其一半的值,然后结合结论(2)即可推出结论;
(4)首先提出假设成立,然后,分情况进行讨论,①若当BE+BF=8,△BEF的面积=
| 1 |
| 3 |
| 28 |
| 3 |
| 2 |
| 3 |
| 56 |
| 3 |
解答: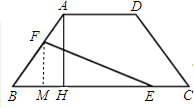 解:(1)∵等腰梯形ABCD中,AB=DC=5,AD=4,BC=10,
解:(1)∵等腰梯形ABCD中,AB=DC=5,AD=4,BC=10,
∴BH=(BC-AD)÷2=3,
∴AH=
=4;
(2)作FM⊥BC于M.
∵等腰梯形ABCD中,AB=DC=5,AD=4,BC=10,
∴等腰梯形ABCD的周长=24,
∵EF平分等腰梯形ABCD的周长,
∴BF+BE=12,
∵BE=x,
∴BF=12-x,
∵FM∥AH,
∴△FBM∽△ABH,
∴BF:AB=FM:AH,
∴
=
,
∴FM=
,
∴△BEF的面积=
•x•
=-
x2+
x;
(3)假设线段EF将等腰梯形ABCD的周长和面积同时平分.
∵等腰梯形ABCD中,AH=4,AD=4,BC=10,
∴等腰梯形ABCD面积的一半=4(4+10)÷2÷2=14,
∵当线段EF将等腰梯形ABCD的周长平分时,△BEF的面积关于x的函数表达式为-
x2+
x,
∴14=-
x2+
x,
∴整理方程得:-x2+12x-35=0,
∵△=b2-4ac=144-140=4>0,
解方程得:x1=5,x2=7,
∵当x1=5,BF=7>AB,
∴x1=5,不符合题意,舍去,
∴当x=7时,线段EF将等腰梯形ABCD的周长和面积同时平分;
(4)假设存在线段EF将等腰梯形ABCD的周长和面积同时分成1:2的两部分.
∵等腰梯形ABCD的周长=24,等腰梯形ABCD的面积=28,
则①若当BE+BF=8,△BEF的面积=
S等腰梯形ABCD=
,
∵BE=x,
∴BF=8-x,
∵FM∥AH,
∴△FBM∽△ABH,
∴BF:AB=FM:AH,
∴
=
,
∴FM=
,
∴△BEF的面积=-
x2+
x,
当
梯形ABCD的面积=
时,
∴
=-
x2+
x,
整理方程得:-3x2+24x-70=0,
∵△=-264<0,故方程无实数解,
∴此种情况不存在,
②若当BE+BF=16,△BEF的面积=
S等腰梯形ABCD=
时,
∴FM=
,
∴△BEF的面积=-
x2+
x,
∴
=-
x2+
x,
整理方程得:-3x2+48x-140=0,
△=b2-4ac=624,
解方程得:x1=
,x2=
(舍去),
∴x=
.
∴当x=
时,线段EF将等腰梯形ABCD的周长和面积同时分成1:2的两部分.
 解:(1)∵等腰梯形ABCD中,AB=DC=5,AD=4,BC=10,
解:(1)∵等腰梯形ABCD中,AB=DC=5,AD=4,BC=10,∴BH=(BC-AD)÷2=3,
∴AH=
| AB2-BH2 |
(2)作FM⊥BC于M.
∵等腰梯形ABCD中,AB=DC=5,AD=4,BC=10,
∴等腰梯形ABCD的周长=24,
∵EF平分等腰梯形ABCD的周长,
∴BF+BE=12,
∵BE=x,
∴BF=12-x,
∵FM∥AH,
∴△FBM∽△ABH,
∴BF:AB=FM:AH,
∴
| 12-x |
| 5 |
| FM |
| 4 |
∴FM=
| 48-4x |
| 5 |
∴△BEF的面积=
| 48-4x |
| 5 |
| 1 |
| 2 |
| 2 |
| 5 |
| 24 |
| 5 |
(3)假设线段EF将等腰梯形ABCD的周长和面积同时平分.
∵等腰梯形ABCD中,AH=4,AD=4,BC=10,
∴等腰梯形ABCD面积的一半=4(4+10)÷2÷2=14,
∵当线段EF将等腰梯形ABCD的周长平分时,△BEF的面积关于x的函数表达式为-
| 2 |
| 5 |
| 24 |
| 5 |
∴14=-
| 2 |
| 5 |
| 24 |
| 5 |
∴整理方程得:-x2+12x-35=0,
∵△=b2-4ac=144-140=4>0,
解方程得:x1=5,x2=7,
∵当x1=5,BF=7>AB,
∴x1=5,不符合题意,舍去,
∴当x=7时,线段EF将等腰梯形ABCD的周长和面积同时平分;
(4)假设存在线段EF将等腰梯形ABCD的周长和面积同时分成1:2的两部分.
∵等腰梯形ABCD的周长=24,等腰梯形ABCD的面积=28,
则①若当BE+BF=8,△BEF的面积=
| 1 |
| 3 |
| 28 |
| 3 |
∵BE=x,
∴BF=8-x,
∵FM∥AH,
∴△FBM∽△ABH,
∴BF:AB=FM:AH,
∴
| 8-x |
| 5 |
| FM |
| 4 |
∴FM=
| 32-4x |
| 5 |
∴△BEF的面积=-
| 2 |
| 5 |
| 16 |
| 5 |
当
| 1 |
| 3 |
| 28 |
| 3 |
∴
| 28 |
| 3 |
| 2 |
| 5 |
| 16 |
| 5 |
整理方程得:-3x2+24x-70=0,
∵△=-264<0,故方程无实数解,
∴此种情况不存在,
②若当BE+BF=16,△BEF的面积=
| 2 |
| 3 |
| 56 |
| 3 |
∴FM=
| 64-4x |
| 5 |
∴△BEF的面积=-
| 2 |
| 5 |
| 32 |
| 5 |
∴
| 56 |
| 3 |
| 2 |
| 5 |
| 32 |
| 5 |
整理方程得:-3x2+48x-140=0,
△=b2-4ac=624,
解方程得:x1=
24-2
| ||
| 3 |
24+2
| ||
| 3 |
∴x=
24-2
| ||
| 3 |
∴当x=
24-2
| ||
| 3 |
点评:本题主要考查等腰梯形的性质、勾股定理、一元二次方程的应用、解直角三角形,关键在于正确的推出FM的长度,和推出用x表示△BEF的面积.

练习册系列答案
相关题目
 25、如图所示,在等腰梯形ABCD中,AD∥BC,AB=CD,点P为BC边上任意一点,且
25、如图所示,在等腰梯形ABCD中,AD∥BC,AB=CD,点P为BC边上任意一点,且 24、已知:如图,在等腰梯形ABCD中,AD∥BC,AB=DC,点E为边BC上一点,且AE=DC.
24、已知:如图,在等腰梯形ABCD中,AD∥BC,AB=DC,点E为边BC上一点,且AE=DC.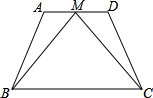 如图,在等腰梯形ABCD中,AD∥BC,M是AD的中点,MB=MC吗?为什么?
如图,在等腰梯形ABCD中,AD∥BC,M是AD的中点,MB=MC吗?为什么? 如图,在等腰梯形ABCD中,AD∥BC,AB=CD,AC⊥BD,垂足为O,过D作DE∥AC交BC的延长线于E.
如图,在等腰梯形ABCD中,AD∥BC,AB=CD,AC⊥BD,垂足为O,过D作DE∥AC交BC的延长线于E.