题目内容
如图,E,B,A,F四点共线,点D是正三角形ABC的边AC的中点,点 是直线
是直线 上异于A,B的一个动点,且满足
上异于A,B的一个动点,且满足 ,则 ( )
,则 ( )

 是直线
是直线 上异于A,B的一个动点,且满足
上异于A,B的一个动点,且满足 ,则 ( )
,则 ( )
A.点 一定在射线 一定在射线 上 上 |
B.点 一定在线段 一定在线段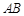 上 上 |
C.点 可以在射线 可以在射线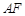 上,也可以在线段 上,也可以在线段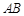 上 上 |
D.点 可以在射线 可以在射线 上,也可以在线段 上,也可以在线段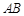 上 上 |
B
分析:连接BD、PC、PD,如图,由等腰三角形的性质可得∠BCD=30°,而∠CPD=30°,可得B、C、D、P四点共圆,于是可得P点的位置.
解答: 解:连接BD、PC、PD,如图,
解:连接BD、PC、PD,如图,
∵△ABC等边三角形,
∴∠CBD=30°,
又∠CPD=30°,
∴∠CBD=∠CPD,
∴B、C、D、P四点共圆,
又∠BDC=90°,
∴点P在以BC为直径的圆上,
∴点P一定在线段AB上.
故选B.
解答:
 解:连接BD、PC、PD,如图,
解:连接BD、PC、PD,如图,∵△ABC等边三角形,
∴∠CBD=30°,
又∠CPD=30°,
∴∠CBD=∠CPD,
∴B、C、D、P四点共圆,
又∠BDC=90°,
∴点P在以BC为直径的圆上,
∴点P一定在线段AB上.
故选B.

练习册系列答案
相关题目


 平移到
平移到 ,则图中平行相等的线段有_____对( )
,则图中平行相等的线段有_____对( )
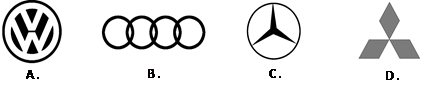



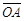 =10, ÐAOB=36°。若固定B点,将此扇形依顺时针方向旋转,得一新扇形A’O’B,其中A点在
=10, ÐAOB=36°。若固定B点,将此扇形依顺时针方向旋转,得一新扇形A’O’B,其中A点在 上,如图(十四)所示,则O点旋转至O’点所经过的轨迹长度为何?
上,如图(十四)所示,则O点旋转至O’点所经过的轨迹长度为何?