题目内容
【题目】填空,完成下列说理过程:
O是直线AB上一点,∠COD = 90°,OE平分∠BOC.
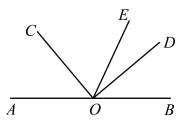
(1)如图1,若∠ AOC = 50°,求∠DOE的度数;
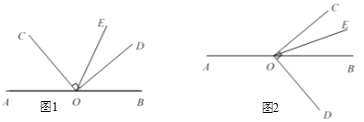
解:∵O是直线AB上一点,
∴∠AOC +∠BOC =180°.
∵∠AOC =50°,
∴∠BOC =130°.
∵OE平分∠BOC(已知),
∴∠COE =![]() ∠BOC ( ).
∠BOC ( ).
∴∠COE = °.
∵∠COD = 90°,∠DOE =∠ ∠ ,
∴∠DOE = °.
(2)将图1中∠ COD按顺时针方向转至图2所示的位置,OE仍然平分∠BOC.试猜想∠AOC与∠DOE的度数之间的关系为: .
【答案】(1)见解析;(2)∠AOC= 2∠DOE.
【解析】
(1)根据角平分线的性质,直角的性质进行解题,(2)根据∠AOB=180°,∠DOC=90°即可解题.
(1)∵O是直线AB上一点,
∴![]() 180°.
180°.
∵![]() =50°,
=50°,
∴![]() =130°.
=130°.
∵OE平分![]() (已知),
(已知),
∴![]() =
=![]()
![]() (角平分线定义)
(角平分线定义)
∴![]() = 65 °.
= 65 °.
∵![]() = 90°,∠ DOE =∠
= 90°,∠ DOE =∠ ![]() ∠
∠ ![]() ,
,
∴![]() = 25 °.
= 25 °.
(2)∠DOE =![]()
![]() (或
(或 ![]() = 2∠DOE) ,
= 2∠DOE) ,
理由:
由题可知,∠AOC+2∠COE=180°,
∠COE+∠DOE=90°,
∴∠AOC+2∠COE=2(∠COE+∠DOE),
整理得:![]() = 2∠DOE
= 2∠DOE

练习册系列答案
相关题目