题目内容
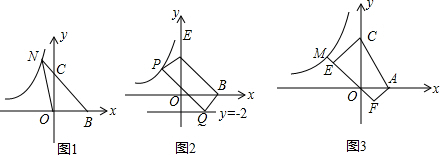
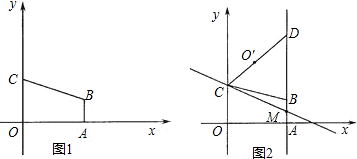
如图1,直线y=-x+4与x轴交于点B,与y轴交于点C,交双曲线 于点N,连ON,且S△OBN=10.
于点N,连ON,且S△OBN=10.
(1)求双曲线的解析式;
(2)如图2,平移直线BC交双曲线于点P,交直线y=-2于点Q,∠FCB=∠QBC,PC=QB求平移后的直线PQ的解析式;
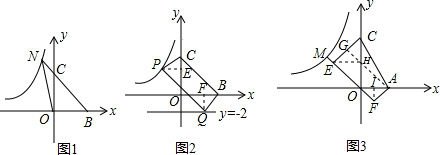
(3)如图3,已知A(2,0)点M为双曲线上一点,CE⊥OM于M,AF⊥OM于F,设梯形CEFA的面积为S,且AF•EF= S,求点M的坐标.
S,求点M的坐标.
 解:(1)∵当y=0时,即-x+4=0,
解:(1)∵当y=0时,即-x+4=0,解得:x=4,
当x=0时,y=4,
∴点B的坐标为:(4,0),点C的坐标为(0,4),
∴OB=OC=4,
∵S△OBN=10,
∴S△OBN=S△OCN+S△OBC=10,
设点N的坐标为(x,y),
∴
 ×4×|x|+
×4×|x|+ ×4×4=10,
×4×4=10,∴x=-1,
∴y=-x+4=1+4=5,
∴点N的坐标为:(-1,5),
∴k=xy=-5,
∴双曲线的解析式为:y=-
 ;
;(2)作PE⊥y轴于E,作QF⊥x轴于F,
则∠PEC=∠QFB=90°,
∵OB=OC,
∴∠OCB=∠OBC,
∵∠PCB=∠QBC,
∴∠PCE=∠QBF,
在△PCE和△QBC中,
∵
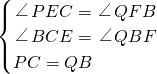 ,
,∴△PCE≌△QBF(AAS),
∴PE=QF=2,
令x=-2,则y=-
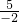 =
= ,
,∴P点的坐标为:(-2,
 ),
),∵PQ∥BC,
∴设直线PQ的解析式为:y=-x+b,
将P(-2,
 )代入得:
)代入得: =2+b,
=2+b,解得:b=
 ,
,∴平移后的直线PQ的解析式为:y=-x+
 ;
;(3)作AG⊥EC于G,交OC于H,作FI⊥OA于I,连接EH,
∵CE⊥EF,FA⊥EF,
∴四边形AFEG是矩形,
∴∠GAF=90°,EG=FA,
∵S=
 (AF+EC)•EF,AF•EF=
(AF+EC)•EF,AF•EF= S,
S,∴AF•EF=
 (AF•EF+EC•EF),
(AF•EF+EC•EF),∴EC=2AF,
∴EG=
 EC,
EC,即EG=GC,
∵GH⊥EC,
∴CH=EH,
∴∠CEH=∠ECH,
∵∠HEO+∠CEH=∠EOH+∠ECH=90°,
∴∠HEO=∠EOH,
∴EH=OH=
 OC=2,
OC=2,∵OA=2,
∴OH=OA,
∴∠HAO=45°,
∴∠OAF=45°,
∴OI=OF=1,
∴点F的坐标为(1,-1),
设直线EF的解析式为:y=kx,
∴k=-1,
∴直线EF的解析式为:y=-x,
联立:
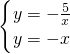 ,
,解得:
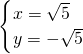 (舍去),
(舍去),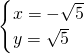 .
.∴点M的坐标为:(-
 ,
, ).
).分析:(1)由直线y=-x+4与x轴交于点B,与y轴交于点C,易求得点B与C的坐标,又由S△OBN=10,即可求得点N的横坐标,继而求得点N的坐标,则可求得双曲线的解析式;
(2)首先作PE⊥y轴于E,作QF⊥x轴于F,易证得△PCE≌△QBF(AAS),则可求得点P的坐标,又由PQ∥BC,利用待定系数法即可求得平移后的直线PQ的解析式;
(3)首先作AG⊥EC于G,交OC于H,作FI⊥OA于I,连接EH,由CE⊥EF,FA⊥EF,可得四边形AFEG是矩形,继而证得AG是EC的垂直平分线,然后可证得CH=EH=OH=2,即可求得OI=FI=1,则可求得点F的坐标,即可得直线EF的解析式,然后与反比例函数联立,即可求得点M的坐标.
点评:此题考查了待定系数法求函数的解析式、反比例函数的性质、全等三角形的判定与性质、等腰直角三角形的判定与性质、等腰三角形的判定与性质以及三角形面积的求解方法等知识.此题综合性很强,难度较大,注意掌握数形结合思想与方程思想的应用.

练习册系列答案
相关题目
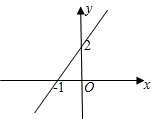 如图,该直线是某个一次函数的图象,则此函数的解析式为
如图,该直线是某个一次函数的图象,则此函数的解析式为
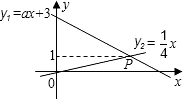 如图,两直线y1=ax+3与y2=
如图,两直线y1=ax+3与y2=