题目内容
如图,已知抛物线y=ax2+bx+c(经过原点)与x轴相交于N点,直线y=kx+4与坐标轴分别相交于 A、D两点,与抛物线相交于B(1,m)和C(2,2)两点.
A、D两点,与抛物线相交于B(1,m)和C(2,2)两点.(1)求直线与抛物线的表达式;
(2)求证:C点是△AOD的外心;
(3)若(1)中的抛物线,在x轴上方的部分,有一动点P(x,y),设∠PON=α.当sinα为何值时,△PON的面积有最大值?
(4)若P点保持(3)中运动路线,是否存在△PON,使得其面积等于△OCN面积的
| 9 | 16 |
分析:(1)由抛物线y=ax2+bx+c经过原点,可得其表达式可以写成y=ax2+bx,又由直线y=kx+4与抛物线相交于B、C两点,把两点的坐标代入y=kx+4,利用待定系数法即可求得直线的表达式与点B与C的坐标,继而求得抛物线的表达式;
(2)由(1)中直线的解析式,求得A与D的坐标,可得AC=CD=OC=
AD,即可得C点是△AOD的外心;
(3)通过分析可得P为顶点时,S△OPN面积最大.求得顶点的坐标,根据正弦函数的定义,即可求得sinα的值;
(4)首先过点P作PE⊥x轴于N点,设点P的坐标为(x,-2x2+5x),即可表示出△PON的面积,然后求得△OCN的面积,由△PON的面积等于△OCN面积的
,即可得方程,解此方程即可求得答案.
(2)由(1)中直线的解析式,求得A与D的坐标,可得AC=CD=OC=
| 1 |
| 2 |
(3)通过分析可得P为顶点时,S△OPN面积最大.求得顶点的坐标,根据正弦函数的定义,即可求得sinα的值;
(4)首先过点P作PE⊥x轴于N点,设点P的坐标为(x,-2x2+5x),即可表示出△PON的面积,然后求得△OCN的面积,由△PON的面积等于△OCN面积的
| 9 |
| 16 |
解答:解:(1)∵抛物线y=ax2+bx+c经过原点,
∴其表达式可以写成y=ax2+bx.
∵直线y=kx+4与抛物线相交于B、C两点,把两点的坐标代入y=kx+4,得:
,
解得:
,
∴直线是:y=-x+4,
点B(1,3),C(2,2)代入二次函数的表达式,得:
,
解得:
,
∴抛物线的表达式为:y=-2x2+5x.
(2)∵y=-x+4,令x=0,y=4;
令y=0,x=4,
∴A(0,4),D(4,0).
∴AD=
=4
.而OC=2
,
∴OC=
AD.
∴C是Rt△AOD的外心.
(3)通过分析知道,P为顶点时,S△OPN面积最大.
此时,P(
,
),
又∵方程-2x2+5x=0的两根是x1=0,x2=
,即ON=
.
∴OP=
=
.
∴sinα=
=
×
=
,此时△PON有最大面积(底是相同的).
(4)存在.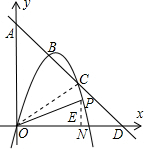
理由:过点P作PE⊥x轴于N点,
设点P的坐标为(x,-2x2+5x),
∴S△OCN=
ON•PD=
×
×(-2x2+5x)=
(-2x2+5x),
∵S△OCN=ON×2×
=ON=
,
又∵△PON的面积等于△OCN面积的
,
∴
(-2x2+5x)=
×
,
解得:x1=
,x2=
,
∴当x=
时,y=
,
当x=
时,y=
,
∴点P的坐标为(
,
)或(
,
).
∴其表达式可以写成y=ax2+bx.
∵直线y=kx+4与抛物线相交于B、C两点,把两点的坐标代入y=kx+4,得:
|
解得:
|
∴直线是:y=-x+4,
点B(1,3),C(2,2)代入二次函数的表达式,得:
|
解得:
|
∴抛物线的表达式为:y=-2x2+5x.
(2)∵y=-x+4,令x=0,y=4;
令y=0,x=4,
∴A(0,4),D(4,0).
∴AD=
| 42+42 |
| 2 |
| 2 |
∴OC=
| 1 |
| 2 |
∴C是Rt△AOD的外心.
(3)通过分析知道,P为顶点时,S△OPN面积最大.
此时,P(
| 5 |
| 4 |
| 25 |
| 8 |
又∵方程-2x2+5x=0的两根是x1=0,x2=
| 5 |
| 2 |
| 5 |
| 2 |
∴OP=
(
|
5
| ||
| 8 |
∴sinα=
| ||||
|
| 25 |
| 8 |
| 8 | ||
5
|
| 5 |
| 29 |
| 29 |
(4)存在.

理由:过点P作PE⊥x轴于N点,
设点P的坐标为(x,-2x2+5x),
∴S△OCN=
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 2 |
| 5 |
| 4 |
∵S△OCN=ON×2×
| 1 |
| 2 |
| 5 |
| 2 |
又∵△PON的面积等于△OCN面积的
| 9 |
| 16 |
∴
| 5 |
| 4 |
| 5 |
| 2 |
| 9 |
| 16 |
解得:x1=
| 1 |
| 4 |
| 9 |
| 4 |
∴当x=
| 1 |
| 4 |
| 9 |
| 8 |
当x=
| 9 |
| 4 |
| 9 |
| 8 |
∴点P的坐标为(
| 1 |
| 4 |
| 9 |
| 8 |
| 9 |
| 4 |
| 9 |
| 8 |
点评:此题考查了一次函数与二次函数的综合应用.此题综合性很强,解题的关键是掌握待定系数法求函数的解析式,掌握点与函数的关系,圆的外心的定义,三角函数以及三角形面积的求解方法等知识.注意数形结合思想与方程思想的应用.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
 C(0,3).
C(0,3). 、C(0,-3)两点,与x轴交于另一点B.
、C(0,-3)两点,与x轴交于另一点B. (2013•衡阳)如图,已知抛物线经过A(1,0),B(0,3)两点,对称轴是x=-1.
(2013•衡阳)如图,已知抛物线经过A(1,0),B(0,3)两点,对称轴是x=-1. 如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,且抛物线经过A(-1,0)、C(0,-3)两点,与x轴交于另一点B.
如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,且抛物线经过A(-1,0)、C(0,-3)两点,与x轴交于另一点B. 如图,已知抛物线y=ax2+bx+c的顶点是(-1,-4),且与x轴交于A、B(1,0)两点,交y轴于点C;
如图,已知抛物线y=ax2+bx+c的顶点是(-1,-4),且与x轴交于A、B(1,0)两点,交y轴于点C;