题目内容
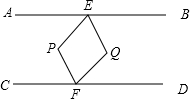
如图，AB∥CD，在AB、CD内有一条折线EPF，∠BEP的平分线与∠DFP的平分线相交于点Q，则∠EPF与∠EQF之间的关系是（ ）
| A．∠EPF+2∠EQF=360° | B．∠EPF-2∠EQF=360° |
| C．2∠EPF+∠EQF=360° | D．2∠EPF-∠EQF=360° |
过点Q作QH∥AB，如图，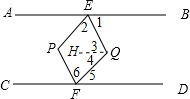
∴∠1=∠3，
∵QE平分∠BEP，
∴∠1=∠2，
∴∠2=∠3，
∵AB∥CD，
∴QH∥CD，
同理可得∠6=∠4，
∴∠EQF=∠PEQ+∠QFP，
∵∠EQF+∠PEQ+∠QFP+∠EPF=360°，
∴∠EPF+2∠EQF=360°．
故选A．
∴∠1=∠3，
∵QE平分∠BEP，
∴∠1=∠2，
∴∠2=∠3，
∵AB∥CD，
∴QH∥CD，
同理可得∠6=∠4，
∴∠EQF=∠PEQ+∠QFP，
∵∠EQF+∠PEQ+∠QFP+∠EPF=360°，
∴∠EPF+2∠EQF=360°．
故选A．
练习册系列答案
口算题天天练系列答案
相关题目
