Question

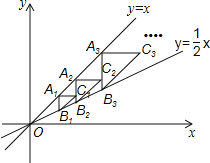
【题目】如图，点在直线上，过点作轴交直线于点，以点为直角顶点，为直角边在的右侧作等腰直角，再过点作轴，分别交直线和于两点，以点为直角项点，为直角边在的右侧作等腰直角…,按此规律进行下去，则等腰直角的面积为___. (用含正整数的代数式表示)

Answer 1

【答案】

【解析】

先根据点A1的坐标以及A1B1∥y轴，求得B1的坐标，进而得到A1B1的长以及△A1B1C1面积，再根据A2的坐标以及A2B2∥y轴，求得B2的坐标，进而得到A2B2的长以及△A2B2C2面积，最后根据根据变换规律，求得AnBn的长，进而得出△AnBnCn的面积即可．

解：∵点A1（2，2），A1B1∥y轴交直线于点B1，

∴B1（2，1）
∴A1B1=2-1=1，即△A1B1C1面积=×12=；
∵A1C1=A1B1=1，
∴A2（3，3），
又∵A2B2∥y轴，交直线于点B2，
∴B2（3，），
∴A2B2=3-=，即△A2B2C2面积=×）2=；
以此类推，
A3B3=，即△A3B3C3面积=×=；
A4B4=，即△A4B4C4面积=×=；
…
∴AnBn=，即△AnBnCn的面积=×=．
故答案为：．