题目内容
【题目】随着“一带一路”的不断建设与深化，我国不少知名企业都积极拓展海外市场，参与投资经营．某著名手机公司在某国经销某种型号的手机，受该国政府经济政策与国民购买力双重影响，手机价格不断下降．分公司在该国某城市的一家手机销售门店，今年5月份的手机售价比去年同期每台降价1000元，若卖出同样多的手机，去年销售额可达10万元，今年销售额只有8万元．
(1)今年5月份每台手机售价多少元？
(2)为增加收入，分公司决定拓展产品线，增加经销某种新型笔记本电脑．已知手机每台成本为3500元，笔记本电脑每台成本为3000元，分公司预计用不少于4.8万元的成本资金少量试生产这两种产品共15台，但因资金所限不能超过5万元，共有几种生产方案？
(3)如果笔记本电脑每台售价3800元，现为打开笔记本电脑的销路，公司决定每售出1台笔记本电脑，就返还顾客现金a元，要使(2)中各方案获利最大，a的值应为多少？最大利润多少？
【答案】(1)今年5月份每台手机售价4000元；(2)5种生产方案；(3)a的值应为300元，最大利润为7500元.
【解析】
（1）设今年5月份手机每台售价为m元，则去年同期每台售价为（m+1000）元，根据数量=总价÷单价结合今年5月份与去年同期的销售数量相同，即可得出关于m的分式方程，解之经检验后即可得出结论；
（2）设生产手机x台，则生产笔记本电脑（15-x）台，根据总价=单价×数量结合总价不少于4.8万元不能超过高于5万元，即可得出关于x的一元一次不等式组，解之即可得出x的取值范围，由该范围内整数的个数即可得出方案的种数；
（3）设总获利为w元，根据利润=销售收入-成本，即可得出w关于x的一次函数关系式，由w的值与x无关，即可得出a-300=0，解之即可求出a值．
（1）设今年5月份手机每台售价为m元，则去年同期每台售价为（m+1000）元，
根据题意得：
，
解得：m=4000，
经检验，m=4000是原方程的根且符合题意．
答：今年5月份手机每台售价为4000元．
（2）设生产手机x台，则生产笔记本电脑（15-x）台，
根据题意得：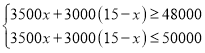
，
解得：6≤x≤10，
∴x的正整数解为6、7、8、9、10．
答：共有5种生产方案．
（3）设总获利为w元，
根据题意得：w=（4000-3500）x+（3800-3000-a）（15-x）=（a-300）x+12000-15a．
∵w的值与x值无关，
∴a-300=0，即a=300．
当a=300时，最大利润为12000-15×300=7500元．
