题目内容
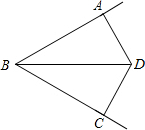如图，已知BD平分∠ABC，AD⊥AB，DC⊥BC，AB=2，AD=1，则DC=1
1
，BC=2
2
．分析：根据角平分线上的点到角的两边的距离相等可得DC=AD，再利用“HL”证明Rt△ABD和Rt△CBD全等，根据全等三角形对应边相等可得BC=AB．
解答：解：∵BD平分∠ABC，AD⊥AB，DC⊥BC，
∴DC=AD=1，
在Rt△ABD和Rt△CBD中，
，
∴Rt△ABD≌Rt△CBD（HL），
∴BC=AB=2．
故答案为：1；2．
∴DC=AD=1，
在Rt△ABD和Rt△CBD中，
|
∴Rt△ABD≌Rt△CBD（HL），
∴BC=AB=2．
故答案为：1；2．
点评：本题考查了角平分线上的点到角的两边的距离相等的性质，全等三角形的判定与性质，是基础题，熟记性质求出DC=AD是解题的关键．
练习册系列答案
相关题目
5、如图，已知BD平分∠ABC，且∠ADE=∠C，那么∠4与∠3的数量关系是（ ）
如图，已知BD平分∠ABC，DE∥AB，∠ABC=70°，BE=3cm，求∠BDE的度数及DE的长度．
如图：已知BD平分∠ABC，EF∥BC交BD于点F，交AB于点E，∠AEF=40°，求∠DFE度数．