题目内容
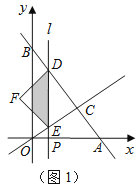
【题目】如图1,直线![]() 分别与
分别与![]() 轴、
轴、![]() 轴交于A、B两点,与直线
轴交于A、B两点,与直线![]() 交于点C(2,
交于点C(2,![]() ).平行于
).平行于![]() 轴的直线l从原点O出发,以每秒1个单位长度的速度沿
轴的直线l从原点O出发,以每秒1个单位长度的速度沿![]() 轴向右平移,到C点时停止;直线l分别交线段BC、OC、
轴向右平移,到C点时停止;直线l分别交线段BC、OC、![]() 轴于点D、E、P,以DE为斜边向左侧作等腰直角△DEF,设直线l的运动时间为
轴于点D、E、P,以DE为斜边向左侧作等腰直角△DEF,设直线l的运动时间为![]() (秒).
(秒).
(1)求![]() 、
、![]() 的值;
的值;
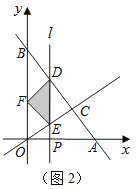
(2)当![]() 为何值时,点F在
为何值时,点F在![]() 轴上(如图2);
轴上(如图2);
(3)设△DEF与△BCO重叠部分的面积为S,请求出S与![]() 的函数关系式,并写出
的函数关系式,并写出![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)当
;(2)当![]() =1时,点F在
=1时,点F在![]() 轴上;(3)当0<t≤1时,S=﹣3t2+4t;当1<t<2时,S=(t﹣2)2.
轴上;(3)当0<t≤1时,S=﹣3t2+4t;当1<t<2时,S=(t﹣2)2.
【解析】分析:(1)利用待定系数法即可求得k和b的值;
(2)当F在y轴上时,F到DE的距离等于DE的长的一半,据此即可列方程求得t的值;
(3)分F在y轴的左侧和右侧两种情况进行讨论,当F在y轴的左侧时,阴影部分是两个等腰直角三角形面积的差,当F在y轴的右侧时,阴影部分就是△DEF的面积,根据三角形的面积公式即可求得函数的解析式.
详解:(1)把(2,![]() )代入y=﹣
)代入y=﹣![]() x+b得:﹣
x+b得:﹣![]() +b=
+b=![]() ,解得:b=4;
,解得:b=4;
把(2,![]() )代入y=kx中,2k=
)代入y=kx中,2k=![]() ,解得:k=
,解得:k=![]() .
.
故答案为:![]() ,4;
,4;
(2)由(1)得两直线的解析式为:
y=﹣![]() x+4和y=
x+4和y=![]() x,依题意得:OP=t,则D(t,﹣
x,依题意得:OP=t,则D(t,﹣![]() t+4),E(t,
t+4),E(t,![]() t),
t),
∴DE=﹣2t+4,作FG⊥DE于G,则FG=OP=t.
∵△DEF是等腰直角三角形,FG⊥DE,∴FG=![]() DE,即t=
DE,即t=![]() (﹣2t+4/span>),解得:t=1.
(﹣2t+4/span>),解得:t=1.
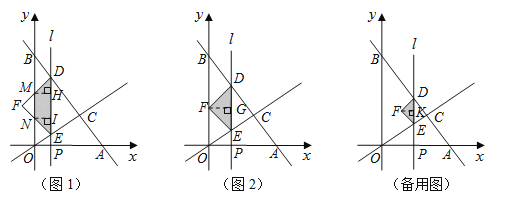
(3)当0<t≤1时(如图1),S△DEF=![]() (﹣
(﹣![]() t+4﹣
t+4﹣![]() t)
t)![]() (﹣
(﹣![]() t+4﹣
t+4﹣![]() t)=
t)=![]() (﹣2t+4)2=(t﹣2)2,在y轴的左边部分是等腰直角三角形,底边上的高是:
(﹣2t+4)2=(t﹣2)2,在y轴的左边部分是等腰直角三角形,底边上的高是:![]() (﹣
(﹣![]() t+4﹣
t+4﹣![]() t)﹣t=
t)﹣t=![]() (﹣2t+4)﹣t=2﹣2t,则面积是:(2﹣2t)2.
(﹣2t+4)﹣t=2﹣2t,则面积是:(2﹣2t)2.
S=(t﹣2)2﹣(2﹣2t)2=﹣3t2+4t;
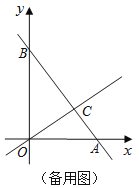
当1<t<2时(备用图),作FK⊥DE于点K.则:
S=(t﹣2)2.
综上所述:当0<t≤1时,S=﹣3t2+4t;当1<t<2时,S=(t﹣2)2.

 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案【题目】列方程解应用题
四川的灾情牵动全国人民的心,某市A、B两个蔬菜基地得知四川C、D两个灾民安置点分别急蔬菜240吨和260吨的消息后,决定调运蔬菜支援灾区。已知A蔬菜基地有蔬菜200吨,B蔬菜基地有蔬菜300吨,现将这些蔬菜全部调往C、D两个灾民安置点。从A地运往C、D两处的费用分别为每吨20元和25元,从B地运往C、D两处的费用分别为每吨15元和18元。设从B地运往C处的蔬菜为![]() 吨。
吨。
(1)请填写下表,并求两个蔬菜基地调运蔬菜的运费相等时![]() 的值?
的值?
C | D | 总计 | |
A | 200吨 | ||
B |
| 300吨 | |
总计 | 240吨 | 260吨 | 500吨 |
(2)已知总运费最小的调运费用是9280元,请你提交具体的调运方案.