Question

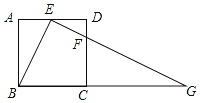
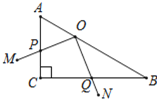
【题目】如图，在Rt△ABC中，∠ACB=90°，∠ABC=30°，直角∠MON的顶点O在AB上，OM、ON分别交CA、CB于点P、Q，∠MON绕点O意旋转．当时．的值为_____．

Answer 1

【答案】

【解析】

如图，过点O作OH⊥AC于H，OG⊥BC于G，由条件可以表示出HO、GO的值，通过证明△PHO∽△QGO由相似三角形的性质就可以求出结论．

解：过点O作OH⊥AC于H，OG⊥BC于G，

∴∠OHP=∠OGQ=90°．
∵∠ACB=90°，
∴四边形HCGO为矩形，
∴∠HOG=90°，
∴∠HOP=∠GOQ，
∴△PHO∽△QGO，
∴．
∵，设OA=x，则OB=2x，且∠ABC=30°，
∴AH=x，OG=x．
在Rt△AHO中，由勾股定理，得
OH= x，
∴ ，
∴．
故答案为：．