题目内容
【题目】如图(1),将两块直角三角尺的直角顶点C叠放在一起, 
(1)若∠DCE=25°,∠ACB=;若∠ACB=150°,则∠DCE=;
(2)猜想∠ACB与∠DCE的大小有何特殊关系,并说明理由;
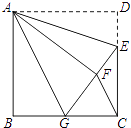
(3)如图(2),若是两个同样的直角三角尺60°锐角的顶点A重合在一起,则∠DAB与∠CAE的大小又有何关系,请说明理由. 
【答案】
(1)155°;30°
(2)解:猜想得:∠ACB+∠DCE=180°(或∠ACB与∠DCE互补)
理由:∵∠ECB=90°,∠ACD=90°
∴∠ACB=∠ACD+∠DCB=90°+∠DCB
∠DCE=∠ECB﹣∠DCB=90°﹣∠DCB
∴∠ACB+∠DCE=180°
(3)解:∠DAB+∠CAE=120°
理由如下:
∵∠DAB=∠DAE+∠CAE+∠CAB
故∠DAB+∠CAE=∠DAE+∠CAE+∠CAB+∠CAE=∠DAC+∠BAE=120°
【解析】解:(1)∵∠ECB=90°,∠DCE=25°
∴∠DCB=90°﹣25°=65°
∵∠ACD=90°
∴∠ACB=∠ACD+∠DCB=155°.
∵∠ACB=150°,∠ACD=90°
∴∠DCB=150°﹣90°=60°
∵∠ECB=90°
∴∠DCE=90°﹣60°=30°.
所以答案是:155°,30°;
【考点精析】解答此题的关键在于理解角的运算的相关知识,掌握角之间可以进行加减运算;一个角可以用其他角的和或差来表示,以及对余角和补角的特征的理解,了解互余、互补是指两个角的数量关系,与两个角的位置无关.

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目