Question

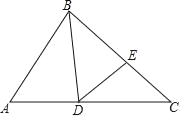
【题目】在正方形ABCD中，E是△ABD内的点，EB=EC．

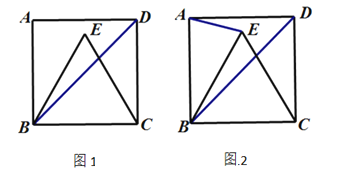
（1）如图1，若EB=BC，求∠EBD的度数；

（2）如图2，EC与BD交于点F，连接AE，若，试探究线段FC与BE之间的等量关系，并说明理由．

Answer 1

【答案】（1）15°；（2）

【解析】

（1）根据等边三角形的性质得∠EBC＝60°，根据正方形的一条对角线平分内角可得∠CBD＝45°，根据角的和与差可得结论；

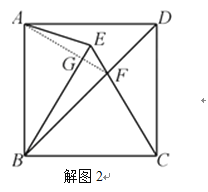
（2）连接AF，证明△ABF≌△CBF（SAS），得AF＝CF，∠BAF＝∠BCF，根据等腰三角形的性质和等式的性质得∠ABE＝∠DCE，从而得∠AGB＝90°，最后利用面积和表示四边形ABFE的面积，可得结论．

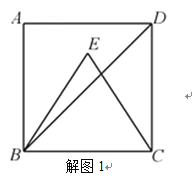
解:如解图1，四边形是正方形，

平分

∴．

,

是等边三角形．

∴∠EBC=60°
°

解:

理由如下:

如解图2，连接与交于点,

四边形是正方形，

．

又

．

,

由得,

又

．

．

在中，

．