题目内容
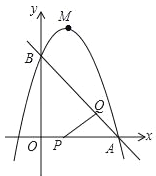
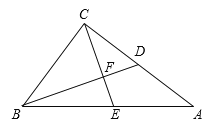
【题目】如图,在![]() 中,
中,![]() ,点
,点![]() 是边
是边![]() 的中点,
的中点,![]() ,垂足为点
,垂足为点![]() ,延长
,延长![]() 与边
与边![]() 交于点
交于点![]() .
.
求:(1)![]() 的正切值;
的正切值;
(2)线段![]() 的长.
的长.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)由Rt△ABC,且CF垂直于BD,利用同角的余角相等得到∠ACE=∠CBD,根据AC的长确定出CD的长,利用锐角三角函数定义求出所求即可;
(2)过点E作EH⊥AC,垂足为点H,在Rt△EHA中,利用锐角三角函数定义表示出tanA,进而表示出AE,在Rt△CEH中,利用锐角三角函数定义表示出CH,由CH+AH表示出AC,根据已知AC的长求出k的值,即可确定出所求.
(1)∵∠ACB=90°,
∴∠ACE+∠BCE=90°,
又∵CF⊥BD,
∴∠CFB=90°,
∴∠BCE+∠CBD=90°,
∴∠ACE=∠CBD,
∵AC=4且D是AC的中点,
∴CD=2,
又∵BC=3,
在Rt△BCD中,∠BCD=90°.
∴tan∠CBD=![]() ,
,
∴tan∠ACE=tan∠CBD![]() ;
;
(2)过点E作EH⊥AC,垂足为点H,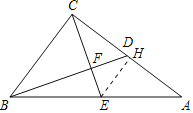
在Rt△EHA中,∠EHA=90°,
∴tanA=![]() ,
,
∵BC=3,AC=4,
在Rt△ABC中,∠ACB=90°,
∴tanA=![]() ,
,
∴![]() ,
,
设EH=3k,AH=4k,
∵![]() ,即
,即![]() ,
,
∴AE=5k,
在Rt△CEH中,∠CHE=90°,
∴tan∠ECA=![]() ,
,
∴CH=![]() ,
,
∴AC=AH+CH=![]() ,
,
解得:![]() ,
,

练习册系列答案
相关题目