题目内容
（2013•黔东南州一模）在Rt△ACB中，∠ACB=90°，设BC=a，AC=b，若a，b是方程x2-7x+7=0的两根，则斜边AB上的中线长为
．
| ||
| 2 |
| ||
| 2 |
分析：利用根与系数的关系求出a+b，ab，然后求出a2+b2，再根据勾股定理求出斜边AB的长，然后根据直角三角形斜边上的中线等于斜边的一半的解答．
解答：解：∵a，b是方程x2-7x+7=0的两根，
∴a+b=7，ab=7，
∴a2+b2=（a+b）2-2ab=49-2×7=35，
∴斜边AB=
=
，
∴斜边AB上的中线长=
．
故答案为：
．
∴a+b=7，ab=7，
∴a2+b2=（a+b）2-2ab=49-2×7=35，
∴斜边AB=
| a2+b2 |
| 35 |
∴斜边AB上的中线长=
| ||
| 2 |
故答案为：
| ||
| 2 |
点评：本题考查了直角三角形斜边上的中线等于斜边的一半的性质，根与系数的关系，勾股定理的应用，以及完全平方公式，求出a2+b2的值是解题的关键．
练习册系列答案
每课必练系列答案
相关题目
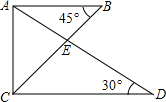（2013•黔东南州）将一副三角尺如图所示叠放在一起，则
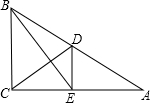（2013•黔东南州一模）如图，在Rt△ABC中，∠ACB=90°，点D是斜边AB的中点，DE⊥AC，垂足为E，若BC=4，CD=2