题目内容
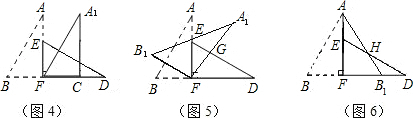
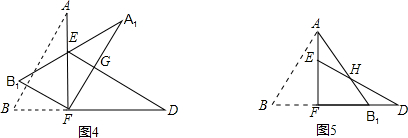
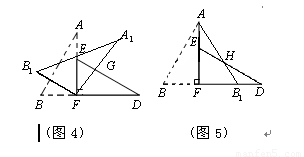
如图1,小明将一张矩形纸片沿对角线剪开,得到两张三角形纸片(如图2),量得他们的斜边长为10cm,较小锐角为30°,再将这两张三角纸片摆成如图3的形状,但点B、C、F、D在同一条直线上,且点C与点F重合.(在图3至图6中统一用F表示)

小明在对这两张三角形纸片进行如下操作时遇到了三个问题,请你帮助解决.
(1)将图3中的△ABF沿BD向右平移到图4的位置,使点B与点F 重合,请你求出平移的距离;
(2)将图3中的△ABF绕点F顺时针方向旋转30°到图5的位置,A1F交DE于点G,请你求出线段FG的长度;
(3)将图3中的△ABF沿直线AF翻折到图6的位置,AB1交DE于点H,请说明:AH=DH.
(1)5cm;(2)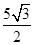 cm;(3)见解析
cm;(3)见解析
【解析】
试题分析:(1)由题意可知AB=10,∠A=30o,根据含30°角的直角三角形的性质可得BF、AF的长,即可求得结果;
(2)由FG⊥DE,可得FG为Rt⊿EFD的高,再根据⊿EFG的面积公式即可求得结果;
(3)由题意可知EF=FB1,AF=FD,则AE=B1D,再结合∠AHE=∠B1HD,∠A=∠D=30o,可得⊿AHE≌⊿DHB1.
即可证得结论.
(1)由题意可知AB=10,∠A=30o
所以BF=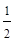 AB=5,AF=
AB=5,AF=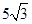
因此平移的距离为BF=5cm;
(2)此时FG⊥DE,故FG为Rt⊿EFD的高.
又因为S⊿EFG=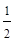 ×10×FG=
×10×FG=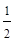 ×
×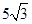 ×5
×5
所以FG=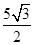 (cm);
(cm);
(3)由题意可知EF=FB1,AF=FD,
所以AE=B1D.
又因为∠AHE=∠B1HD,∠A=∠D=30o,
所以⊿AHE≌⊿DHB1.
故AH=DH.
考点:含30°角的直角三角形的性质,三角形的面积公式,全等三角形的判定和性质
点评:本题知识点多,综合性强,需要学生熟练平面图形的各种基本知识.

 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案