题目内容
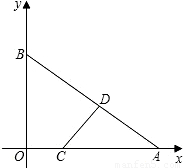
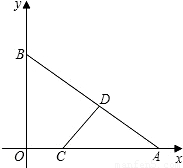
(2004•十堰)在平面直角坐标系xoy中,以O为原心,12为半径作圆交x轴于E,F两点,交y轴千C,D两点,G为劣弧 上一点.且
上一点.且 .
.(1)求G点的坐标;
(2)求过G、E、F三点的抛物线的解析式;
(3)点A为x轴正半轴上一点,且在圆O的外部,过A作圆O的一条切线AB,切点为B,交y轴正半轴于点H,若以点A、O、H为顶点的三角形与三角形EGF相似,求AF的长.

【答案】分析:(1)本题可通过构建直角三角形来求G点的坐标,过G作GG′⊥x轴于G′,那么根据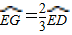 ,可知∠GOE=60°,在直接三角形GOG′中,可根据半径的长和∠GOE的度数求出G点的坐标;
,可知∠GOE=60°,在直接三角形GOG′中,可根据半径的长和∠GOE的度数求出G点的坐标;
(2)已知了圆的半径,易知E,F的坐标为(-12,0),(12,0).因此可用待定系数法求出抛物线的解析式;
(3)连接OB,已知了∠GEF=60°,那么本题可分两种情况进行讨论:
①∠HAO=60°,那么在直角三角形OBA中,根据半径的长和∠BAO的度数即可求出OA的长,也就能求出AF的长.
②∠HAO=30°,方法同①.
解答: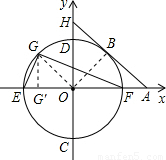 解:(1)过点G作GG'⊥x轴,垂足为G',
解:(1)过点G作GG'⊥x轴,垂足为G',
由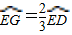 有:∠GOE=60,GG'=6
有:∠GOE=60,GG'=6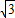 ,OG'=6,
,OG'=6,
∴G(-6,6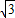 );
);
(2)设过G、E、F三点的抛物线的解析式为y=ax2+bx+c(a≠0),
由己知有:E(-12,0),F(12,0),
将G、E、F三点的坐标代入y=ax2+bx+c(a≠0)
有: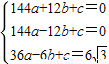 ,
,
解之得: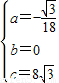 .
.
∴过G、E、F三点的抛物线的解析式为y=-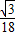 x2+8
x2+8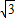 ;
;
(3)连接OB,则OB⊥AH,由己知有∠GFE=30°,∠GEF=60°
要使以点A、O、H为顶点的三角形与三角形EGF相似,
必须满足∠HAO=30°,或∠HAO=60°
(i)若∠HAO=30°,则OA=2,OB=24,
∴AF=24-12=12.
(ii)若∠HAO=60°,则OB=OAsin60°=12,OA=8 ,
,
∴AF=8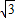 -12.
-12.
点评:本题着重考查了待定系数法求二次函数解析式、相似三角形的判定和性质等重要知识点,要注意的是(3)中,在不确定相似三角形哪些角是对应角的情况下要分类讨论,不要漏解.
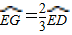 ,可知∠GOE=60°,在直接三角形GOG′中,可根据半径的长和∠GOE的度数求出G点的坐标;
,可知∠GOE=60°,在直接三角形GOG′中,可根据半径的长和∠GOE的度数求出G点的坐标;(2)已知了圆的半径,易知E,F的坐标为(-12,0),(12,0).因此可用待定系数法求出抛物线的解析式;
(3)连接OB,已知了∠GEF=60°,那么本题可分两种情况进行讨论:
①∠HAO=60°,那么在直角三角形OBA中,根据半径的长和∠BAO的度数即可求出OA的长,也就能求出AF的长.
②∠HAO=30°,方法同①.
解答:
 解:(1)过点G作GG'⊥x轴,垂足为G',
解:(1)过点G作GG'⊥x轴,垂足为G',由
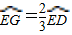 有:∠GOE=60,GG'=6
有:∠GOE=60,GG'=6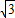 ,OG'=6,
,OG'=6,∴G(-6,6
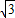 );
);(2)设过G、E、F三点的抛物线的解析式为y=ax2+bx+c(a≠0),
由己知有:E(-12,0),F(12,0),
将G、E、F三点的坐标代入y=ax2+bx+c(a≠0)
有:
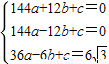 ,
,解之得:
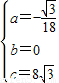 .
.∴过G、E、F三点的抛物线的解析式为y=-
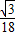 x2+8
x2+8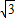 ;
;(3)连接OB,则OB⊥AH,由己知有∠GFE=30°,∠GEF=60°
要使以点A、O、H为顶点的三角形与三角形EGF相似,
必须满足∠HAO=30°,或∠HAO=60°
(i)若∠HAO=30°,则OA=2,OB=24,
∴AF=24-12=12.
(ii)若∠HAO=60°,则OB=OAsin60°=12,OA=8
 ,
,∴AF=8
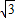 -12.
-12.点评:本题着重考查了待定系数法求二次函数解析式、相似三角形的判定和性质等重要知识点,要注意的是(3)中,在不确定相似三角形哪些角是对应角的情况下要分类讨论,不要漏解.

练习册系列答案
相关题目
 上一点.且
上一点.且 .
.