Question

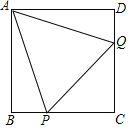
【题目】如图，正方形ABCD中，AB＝1，以线段BC、CD上两点P、Q和方形的点A为顶点作正方形的内接等边△APQ，求△APQ的边长．

Answer 1

【答案】△APQ的边长为．

【解析】

连接AC，交PQ于点H，根据正方形和等边三角形的性质可证Rt△ABP≌Rt△ADQ，可得△CPQ是等腰直角三角形，在直角三角形ABP中，解直角三角形可求得PH，即可求得△APQ的边长.

连接AC，交PQ于点H，

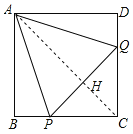
如图所示：则∠BAC＝∠DAC＝∠BCA＝∠DCA＝45°，

∵△APQ是等边三角形，

∴AP＝AQ＝PQ，∠PAQ＝60°，

∵四边形ABCD是正方形，

∴AB＝AD，∠B＝∠D＝90°，

在Rt△ABP和Rt△ADQ中，，

∴Rt△ABP≌Rt△ADQ（HL），

∴∠BAP＝∠DAQ，BP＝DQ，

∴∠PAC＝∠QAC，CP＝CQ，

∴△CPQ是等腰直角三角形，

∵∠PAQ＝60°，

∴∠PAC＝∠QAC＝30°，

∵∠APQ＝60°，

∴∠AHP＝90°，

∴PH＝QH，

∴CH＝PH＝QH，AC＝AB＝，

PH＝tan∠PAHAH＝tan30°×（AC﹣CH）＝×（﹣PH），

解得：PH＝，

∴PQ＝2PH＝，

∴△APQ的边长为．