题目内容
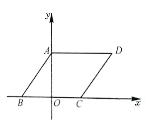
【题目】如图,平行四边形ABCD在平面直角坐标系中,AD=6,若OA,OB的长是关于x的一元二次方程![]() 的两个根,且OA>OB.
的两个根,且OA>OB.
(1)若点E为x轴上的点,且△AOE的面积为![]() .
.
求:①点E的坐标;②证明:△AOE∽△DAO;
(2)若点M在平面直角坐标系中,则在直线AB上是否存在点F,使以A,C,F,M为顶点的四边形为菱形?若存在,请直接写出F点的坐标;若不存在,请说明理由.
【答案】(1)①![]() 或
或![]() ;②详见解析;(2)
;②详见解析;(2)![]()
【解析】
(1)①解一元二次方程求出OA,OB的长度,根据三角形的面积求出点E的坐标.
②分别求出两三角形夹直角的两对应边的比,如果相等,则两三角形相似,否则不相似;
(2)根据菱形的性质,分AC与AF是邻边并且点F在射线AB上与射线BA上两种情况,以及AC与AF分别是对角线的情况分别进行求解计算.
(1)![]()
(x3)(x4)=0,
∴x3=0,x4=0,
解得![]()
∵OA>OB,
∴OA=4,OB=3,
∵![]()
∴![]()
∴![]()
∵点E在x轴上
∴E点的坐标为![]() 或
或![]()
②在△AOE与△DAO中, AD=6,
![]()
![]()
∴![]()
又∵![]()
∴△AOE∽△DAO;
(2)根据计算的数据,OB=OC=3,
∴AO平分∠BAC,
①AC、AF是邻边,点F在射线AB上时,AF=AC=5,
所以点F与B重合,
即F(3,0),
②AC、AF是邻边,点F在射线BA上时,M应在直线AD上,且FC垂直平分AM,
点F(3,8).
③AC是对角线时,做AC垂直平分线L,AC解析式为![]() ,直线L过
,直线L过![]() 且k值为
且k值为![]() (平面内互相垂直的两条直线k值乘积为1),
(平面内互相垂直的两条直线k值乘积为1),
L解析式为![]() 联立直线L与直线AB求交点,
联立直线L与直线AB求交点,
∴F![]() ;
;
④AF是对角线时,过C做AB垂线,垂足为N,根据等积法求出![]() 勾股定理得出,A
勾股定理得出,A![]() 做A关于N的对称点即为F,
做A关于N的对称点即为F,![]() 过F做y轴垂线,垂足为G,
过F做y轴垂线,垂足为G,
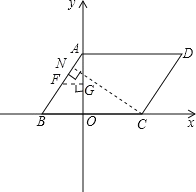
![]()
∴F![]()
综上所述,满足条件的点有四个:![]()

 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案