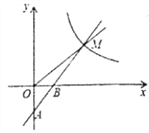
题目内容
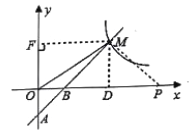
【题目】如图,一次函数![]() 的图象经过
的图象经过![]() 、
、![]() 两点,与反比例函数的图象在第一象限内交于点M,△OBM的面积为2.
两点,与反比例函数的图象在第一象限内交于点M,△OBM的面积为2.
(1)求一次函数和反比例函数的表达式;
(2)求AM的长度;
(3)P是x轴上一点,当AM⊥PM时,求出点P的坐标.
【答案】(1)![]() ;(2)
;(2) ![]() ;(3)(11,0)
;(3)(11,0)
【解析】试题分析: (1)根据一次函数y=k1x+b的图像经过A、B可得b、k1的方程组,进而求得一次函数的解析式,设M(m,n)作MD⊥x轴于点D,由△OBM的面积为2可求出n的值,将M(m,4)代入y=2x-2求出m的值,由M点在双曲线上求出k2,进而得到反比例函数的解析式;
(2)根据已知构造直角三角形进而利用勾股定理求出AM的长;
(3)过点M作MP⊥AM交x轴于点P,由MD⊥BP求出∠PMD=∠MBD=∠ABO,再由锐角三角形函数的定义求出OP的值,进而可得出结论.
试题解析:(1)∵直线![]() 的图象经过
的图象经过![]() 、
、![]() 两点
两点
∴![]() ,
,
∴解得: ![]()
∴一次函数的表达式为![]() ,
,
∴设![]() ,作MD⊥x轴于点D
,作MD⊥x轴于点D
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴n=4,
∴将![]() 代入
代入![]() 得
得![]() ,
,
∴m=3
∵![]() 在双曲线
在双曲线![]() 上,
上,
∴![]() ,
,
∴![]() ,
,
∴反比例函数的表达式为: ![]() ;
;
则FM=3,AF=4+2=6,
∴![]() ;
;
(3)过点![]() 作MP⊥AM交x轴于点P,
作MP⊥AM交x轴于点P,
∵MD⊥BP,
∴∠PMD=∠MBD=∠ABO
∴![]() ,
,
∴在Rt△PDM中, ![]() ,
,
∴PD=2MD=8,
∴OP=OD+PD=11
∴当PM⊥AM,此时点P的坐标为(11,0).

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目