题目内容
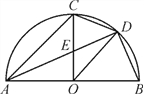
【题目】如图AB是半圆O的直径，半径OC⊥AB于点O，AD平分∠CAB分别交OC于点E，交弧BC于点D，连结CD、OD，给出以下5个结论：①OD∥AC；②AC＝2CD；③2CD2＝CEAB；④S△AEC＝2S△DEO；⑤线段OD是DE与DA的比例中项．其中正确结论的序号( )
A. ①②③ B. ①④⑤ C. ①③④ D. ①③④⑤
【答案】C
【解析】
根据“圆的相关性质和相似三角形的判定与性质”结合已知条件进行分析判断即可.
（1）∵AD平均∠CAB，
∴∠CAD=∠BAD，
∵OA=OD，
∴∠BAD=∠ADO，
∴∠CAD=∠ADO，
∴OD∥AC，即结论①成立；
（2）连接BC，∵OC⊥AB，
∴AC=BC，
∵AD平均∠BAC，
∴点D是
的中点，
∴CD=BD，
∵在△BCD中，CD+BD>BC，
∴2CD>BC，
∴2CD>AC，即结论②不成立；
（3）∵OC⊥AB，
∴∠AOC=∠BOC=90°，
∴∠CDE=
∠AOC=45°，
∵点D是的中点，
∴∠COD=∠BOC=45°，
∴∠CDE=∠COD，
又∵∠DCE=∠OCD，
∴△CDE∽△COD，
∴CD：CO=CE：CD，
∴CD2=CE·CO，
∵CO=AO=AB，
∴CD2=CE·AB，
∴2CD2=CE·AB，即结论③成立；
（4）∵AC∥OD，
∴△ACE∽△DOE，
∴S△ACE：S△DOE=
，
∵△AOC中，∠AOC=90°，OA=OC，
∴AC：OC=
，
∴S△ACE：S△DOE=2：1，
∴S△ACE=2S△DOE，即结论④成立；
（5）∵在△AOD中，AO=DO，∠AOD=∠AOC+∠COD=135°，
∴∠OAD=∠ODA=22.5°，
∵在△DOE中，∠DOE=45°，∠ODE=22.5°，
∴∠DEO=180°-45°-22.5°=112.5°，
由此可知△AOD是等腰三角形，而△DOE不是等腰三角形，
∴△AOD和△OED不可能相似，
∴无法证明OD是AD和DE的比例中项，即结论⑤不成立.
综上所述，上述5个结论中，成立的是①③④.
故选C.
